《高等数学》课程教学资源（课件讲稿）2.5 函数的微分

第五节函数的微分一、微分的定义可微的条件三微分的几何意义四、微分公式与微分运算法则五、微分在近似计算中的应用

第五节 函数的微分 一、微分的定义 三、微分的几何意义 五、微分在近似计算中的应用 二、可微的条件 四、微分公式与微分运算法则

第二章导数与积分一、微分的定义引例正方形金属薄片受热后面积的改变量(Dr)设边长由变到+口：正方形面积A=xo2,： （+一中A=Xa=2（(2)(1)(1)：的线性函数且为的主要部分；(2)：△x的高阶无穷小，当|△x很小时可忽略第五节函数的微分

第五节 函数的微分 第二章 导数与积分 一、微分的定义 引例 正方形金属薄片受热后面积的改变量. (1) (2) 设边长由ᵽ0变到ᵽ0 + ,ᵽ ᵽ ᵽ ∴ ᵽ= (ᵽ0 + ᵽ) 2 − ᵽ2 0 = 2ᵽ0 ⋅ ᵽ+ (ᵽ) 2 . ᵽ0 ᵽ ᵽ0 ᵽ (1): ᵽ的线性函数,且为ᵽ的主要部分; (2):

第二章导数与积分微分定义设函数手0在某区间内有定义及+在这区间内如果（+口（=0成立（其中是与无关的常数）则称函数在点日可微，并且称A△x为函数y=f（x）在点x相应于自变量增量△x的微分，记作dyl或df(xo），即dyl= A·△x.微分四做函数增量的线性主部，（微分的实质）第五节函数的微分

第五节 函数的微分 第二章 导数与积分 微分定义 (微分的实质) 如果 设函数ᵽ= ᵽ(ᵽ)在某区间内有定义, ᵽ0及ᵽ0 + ᵽ在这区间内, 可微， ᵽ= ᵽ(ᵽ0 + ᵽ) − ᵽ(ᵽ0) = ᵽ⋅ ᵽ+ ᵽ(ᵽ) 成立(其中是与ᵽ ᵽ无关的常数),则称函数ᵽ= ᵽ(ᵽ)在点ᵽ0   微分ᵽ叫做函数增量ᵽ的线性主部.  ᵽ= ᵽ0 ᵽ= ᵽ0

第二章导数与积分可微的条件定理函数在点可微的充要条件是函数0在点处可导且 ),证充分性必要性Ayf'(xo) = lim：（在点6可微，4x-0△xAy=f'(xo)+α(lim α=0)△xAX-0Ay0(4x)limA+ lim:.口中-甲△x△x=0△x4x→0线性主部高阶无穷小：（在可导且年：（在点可微第五节函数的微分

第五节 函数的微分 第二章 导数与积分 定理 一、可微的条件 证 必要性. 充分性. 线性主部 高阶无穷小 函数ᵽ(ᵽ)在点ᵽ0可微的充要条件是函数ᵽ(ᵽ)在点ᵽ0处可导, 且 ᵽ= ᵽ′ (ᵽ0). ∵ ᵽ(ᵽ)在点ᵽ0可微, ∴ ᵽ= ᵽ⋅ ᵽ+ ᵽ(ᵽ), = ᵽ ∴ ᵽ(ᵽ)在ᵽ0可导,且ᵽ= ᵽ′(ᵽ0 ). ᵽ= ᵽ′(ᵽ0 ) ⋅ ᵽ+ ᵽ⋅ (ᵽ) ∴ ᵽ(ᵽ)在点ᵽ0可微. 第五节 函数的微分 第二章 导数与积分

第二章导数与积分由上述可知：(可导→可微，且甲相口Ay - dy=0.即lim（日日是比高阶无穷小△x4x-0Ay即lim（当）≠0时与是等价无穷小=1x-0 dy(4）当|△x|很小时，dy是Ay的线性主部，即EAy1Ay = dy + o(dy) ≤ limAx-0 dy（有限增量公式（+一（）～相）口第五节函数的微分

第五节 函数的微分 第二章 导数与积分 由上述可知: (ᵽ)  可导⇔可微, 且ᵽ= ᵽ′ (ᵽ0)ᵽ. (ᵽ)  ᵽ− ᵽ= ᵽ(ᵽ)是比ᵽ高阶无穷小, (ᵽ) 当ᵽ′ (ᵽ0) ≠ 0时,ᵽ与是等价无穷小 ᵽ , 即ᵽ≈ ᵽ. (ᵽ) 有限增量公式 ᵽ(ᵽ0 + ᵽ) − ᵽ(ᵽ0) ≈ ᵽ′ (ᵽ0)ᵽ. 第五节 函数的微分 第二章 导数与积分

第二章导数与积分例2求函数手当手2，手002时的微分，解：甲（=32x=2x =2=3x24xdy4x = 0.02 = 024.△x = 0.02通常把自变量x的增量△x称为自变量的微分，记作dx，即dx=△xdy:台f'(x)dx即函数的微分dy与自变量的微分dx之商等于该函数的导数.导数也叫“微商”第五节函数的微分

第五节 函数的微分 第二章 导数与积分 例2 解 求函数 ᵽ= ᵽ3 当ᵽ= 2,  ᵽ= 0.02时的微分. ∵ ᵽ= (ᵽ3) ′ᵽ = 3ᵽ2ᵽ. = 0.24. ∴ ᵽ= ᵽ′(ᵽ)ᵽ

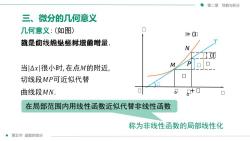
第二章导数与积分三、 微分的几何意义口几何意义：（如图）E(中7就是懒线嫩纵标忆剪蜡量N15P口M当|△x很小时，在点M的附近口切线段MP可近似代替口口0曲线段MN.口在局部范围内用线性函数近似代替非线性函数称为非线性函数的局部线性化第五节函数的微分

第五节 函数的微分 第二章 导数与积分 三、微分的几何意义 ᵽ= ᵽ(ᵽ) ᵽ0 M N T ᵽ ᵽ ᵽ(ᵽ) ） ᵽ ᵽ ᵽ ᵽ 几何意义:(如图) ᵽ0 +ᵽ P 称为非线性函数的局部线性化 当ᵽ就是切线纵坐标对应的增量 ᵽ是曲线的纵坐标增量时, . 在局部范围内,用线性函数近似代替非线性函数 ᵽ

第二章导数与积分四、微分公式与微分运算法则F求法：计算函数的导数，乘以自变量的微分1.基本初等函数的微分公式d(C) = 0d(xμ) = μxu-1dxd(sin x) = cos x dxd(cos x) = - sin x dxd(tan x) = sec2 x dxd(cotx) = - csc2 x dxd(sec x) = sec x tan x dxd(cscx) = - csc x cot x dx第五节函数的微分

第五节 函数的微分 第二章 导数与积分 四、微分公式与微分运算法则 1. 基本初等函数的微分公式 ᵽ= ᵽ′ (ᵽ)ᵽ

第二章导数与积分d(ax) = ax Inadxd(ex) = e*dx11dxd(loga x)d(ln x) ==dxxIn ax11dxd(arcsin x)dxd(arccos x)V1 - x2V1 - x211dxd(arctan x)dxd(arccot x) :1 + x21 +x22.函数和、亲差、积、商的微分法则d(Cu) = Cdud(u±)=du±dvvdu- udvd(uv) = vdu + udvv2第五节函数的微分

第五节 函数的微分 第二章 导数与积分 2. 函数和、差、积、商的微分法则

第二章导数与积分设y= ln(x+ex2),求dy例4 y'=1+ 2xe+21+2xex2解dxx+ex2, : dy=x+ex?例5设 y= e1-3xcosx, 求dy.解dy = cos x · d(e1-3x) +e1-3x .d(cosx).: (e1-3x)'=-3el-3x,(cosx)'=-sinx.: dy=cosx· (-3e1-3x)dx +e1-3x.(-sinx)dx=- e1-3x(3cos x +sin x)dx.第五节函数的微分

第五节 函数的微分 第二章 导数与积分 例4 解 例5 解