《高等数学》课程教学资源（课件讲稿）1.5 极限运算法则

第五节极限运算法则一、无穷小运算法则极限的四则运算法则三、求极限方法举例四、复合函数的极限运算法则

第五节 极限运算法则 一、无穷小运算法则 二、极限的四则运算法则 三、求极限方法举例 四、复合函数的极限运算法则

第一章函数与极限本节符号说明本节中的部分定理和推论，虽以记号“lim"呈现，但对于自变量的各种变化过程都是成立的在论证时，只证明了x一x的情形，对于x一→>0时的证明，类似可证．例如：只要把改成X，把0X即可.第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 本节符号说明 本节中的部分定理和推论，虽以记号“lim”呈 现，但对于自变量的各种变化过程都是成立的. 在论证时，只证明了x→x0的情形，对于x→∞时 的证明，类似可证. 例如∶ 只要把δ改成X，把0X 即可

第一章函数与极限一、无穷小运算法则定理1两个无穷小的和还是无穷小，证考虑两个无穷小的和.设α=α(×)，β=β(×)都为无穷小则Elim α=0→0,>0,当 00, 当0< Ix-xol <2 时,有Iβl <2x-xo取=min81,82},则当0<lx-xol<时,有<+口=口因此 ,m(α + β) = 0. lα+β≤αl+Iβl2 2得证这说明当时，口为无穷小量类似可证：有限个无穷小之和仍为无穷小第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 一、无穷小运算法则 定理1 两个无穷小的和还是无穷小 . 类似可证: 有限个无穷小之和仍为无穷小 . 证 考虑两个无穷小的和. ∀ᵼ> 0, 当 当 取 则当 因此 这说明当 ᵼ→ᵼ0 ᵼ+ ᵼ 为无穷小量 . ∃ᵼ1 > 0, ∃ᵼ2 > 0, 0, 设α = α(x),  β = β(x)都为无穷小,则 得证. 第五节 极限运算法则 第一章 函数与极限

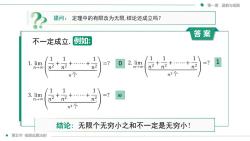
第一章函数与极限提问：定理中的有限改为无限，结论还成立吗？答案例如：不一定成立111112. lim=?1. lim=?+n222n22n2n2n-8n-00n2n1113. lim=?82h2n2n-→00n3个结论：无限个无穷小之和不一定是无穷小！第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 不一定成立. 答 案 例如: 结论: 无限个无穷小之和不一定是无穷小! 0 1 ∞

第一章函数与极限定理2有界函数与无穷小的乘积是无穷小，（常用）证设u=u(x)有界α=α(x)为无穷小u有界→Vx E U (xo, S1),有lul≤M.lim α=0—→0, >0,当× (xo, 82)时,有lαl≤Mx-xo取=min[81，82),则当u(口时,就有[uαl =ulα|≤口故limuα=0,即是时的无穷小，得证X→x0推论1常数与无穷小的乘积是无穷小推论2有限个无穷小的乘积是无穷小第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 第五节 极限运算法则 第一章 函数与极限 推论2 有限个无穷小的乘积是无穷小. 定理2 有界函数与无穷小的乘积是无穷小.（常用） 推论1 常数与无穷小的乘积是无穷小. 证 当 取 则当 故 即 是 时的无穷小. ≤ ᵼ⋅ ᵼ ᵼ = ᵼ, ∀ᵼ> 0, ∃ᵼ2 > 0, ᵼ ᵼ→ᵼ0 u有界 有 设u = u(x)有界,α = α(x)为无穷小. 得证. ᵼ∈    (ᵼ0 , ᵼ)

第一章函数与极限极限的四则运算法则定理3如果limf(x)= A,limg(x)= B,则有(1)lim[f(x)±g(x)l = limf (x)± limg (x) =田 (2) lim[f(x) ·g(x)] = limf (x)· limg (x)=吕口f(x)limf (x)(3）若又有B≠0,则limlimf (x)口g(x)注(1）和(2)的结论均可推广到有限多项的情形例如：lim[f(x) + g(x) - h(x)l = lim f (x) + limg (x) - lim h(x)lim[f(x) ·g(x) - h(x)) = limf (x) · limg (x) · limh(x)第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 第五节 极限运算法则 第一章 函数与极限 二、极限的四则运算法则 定理3 则有 = ᵼ± ᵼ. = ᵼ⋅ ᵼ. （3）若又有B ≠ 0, = ᵼ ᵼ . 注 (1)和(2)的结论均可推广到有限多项的情形. 例如:

第一章函数与极限证：现在给出定理3的证明(1)即证lim[f(x)±g(x))=limf(x)±limg(x) limf (x) = A, limg(x) = B,：f(x)=A+α，g(x)=B+β，其中α，β为无穷小于是f(x)±g(x)=(A+α)±(B+β)=(A±B)+(α±β)又：α±β是无穷小，得证: lim[f(x)±g(x)) = A± B = limf (x) ±limg(x).第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 证 现在给出定理3的证明. 于是 其中α , β为无穷小. 又 ∵ α±β是无穷小, 得证

第一章函数与极限证（2）即证lim[f(x)·g(x))=limf(x)·limg(x).: limf (x) = A, limg(x) = B,：f(x)=A+α,g(x)=B+β,其中αβ为无穷小00于是=为无穷小又:limAβ=olimBα=O,limαβ=0想想为什么？:. lim(Aβ + Bα +αβ) = 0,得证. lim[f(x) ·g(x)) = A ·B= lim f (x) · limg(x).极限存在必有界有界函数与无穷小的乘积仍为无穷小两个无穷小的乘积仍为无穷小第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 第五节 极限运算法则 第一章 函数与极限 证 得证. 想想为什么？ 于是 其中α,β为无穷小. ᵼ(ᵼ) ⋅ᵼ(ᵼ) = (ᵼ+ ᵼ) ⋅ (ᵼ+ ᵼ) = ᵼᵼ+ (ᵼ+ ᵼ+ ᵼᵼ). 又 为无穷小 • 极限存在必有界 • 有界函数与无穷小的乘积仍为无穷小 • 两个无穷小的乘积仍为无穷小

第一章函数与极限f(x)limf (x)证（3）即证lim其中lim g(x) ± 0.limg(x)g(x): lim f (x) = A, limg(x) = B,：f(x)=A+α,g(x)=B+β,其中α，β为无穷小Af(x)(A+αA)A+α1A+(Bα- Aβ)IB于是g(x)BB + β(B +βBB(B +β)需证它为无穷小: lim(Bα - Aβ) = 0,1局部有界：只需证明B(B+β)下面就x→xo情形给出证明，其他情形类似可得第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 第五节 极限运算法则 第一章 函数与极限 证 于是 其中α , β为无穷小. 需证它为无穷小

第一章函数与极限B又 lim=g(x) = B, 8 >0, 当xEs(xo)时,有lg(x)≥2X→X01112[B|2[B|B(B +β)g(x)1即在xo的去心8领域Us(xo)内有界B(B +β)1..lim(Bα - Aβ) = 0.B(B +β)X→xo1Af(x)lim f (x)得证其中limg(x)=B≠0...limBlim g(x)g(x)第五节极限运算法则

第五节 极限运算法则 第一章 函数与极限 第五节 极限运算法则 第一章 函数与极限 又 得证