《复变函数与积分变换》课程教学课件（PPT讲稿）总复习

本课程的总复习以及不足研究对象：复变函数研究内容：复变函数的性质研究方法：分析（微分积分）、代数（级数）

本课程的总复习以及不足 研究对象：复变函数 研究内容：复变函数的性质 研究方法：分析（微分积分）、代数（级数）

首先，跟同学们道：这学期由于家庭原因导致没能从头到屋为大家上课，好在有赵涛还有刘玉锦两位老师的帮助，还有同学们的努力，我们的课程结尾虽有点仓促，不过最后还是顺利结课。其次，考试总共有四大题：1.判断题2.填空题3.计算题4.综合题“总复习”涵盖了此次考试的大部分知识点，应该会对大家有所帮助。希望大家取得好成绩最后，祝大家元旦快乐

首先，跟同学们道歉：这学期由于家庭原因导致没能从头到尾 为大家上课，好在有赵涛还有刘玉锦两位老师的帮助，还有同 学们的努力，我们的课程结尾虽有点仓促，不过最后还是顺利 结课。 其次，考试总共有四大题： 1.判断题 2.填空题 3.计算题 4.综合题 ‘总复习’涵盖了此次考试的大部分知识点，应该会对大家有 所帮助。希望大家取得好成绩。 最后，祝大家元旦快乐

微分：dwdf(z)f(zo +△z)- f(zo): limf'(z.-20=20dzdz4z0△z定义若函数(z)在点z的邻域内处处可导，则称(z)在点z.解析若函数(z)在区域D内每一点都解析，则称(z)在区域D内解析。定理设函数(z)=u(x,y)+iv(x,y)在区域D内有定义，则(z)在区域D内一点z-x+iy可导的充要条件是(1)二元实函数u(x,y)和v(x,y)在点(x,y)可微;(2)u(x,y),v(x,y)在点(x,y)满足柯西-黎曼方程ouvQuavOxOxayay

微分： 0 0 0 0 0 Δ 0 d ( ) d ( Δ ) ( ) ( ) . lim d d Δ z z z z z f z w f z z f z f z z z z = = → + −  = = = 定义 若函数f(z)在点z0的邻域内处处可导，则称f(z)在点z0解析. 若函数f(z)在区域D内每一点都解析，则称f(z)在区域D内解析。 定理 设函数f(z)=u(x,y)+iv(x,y)在区域D内有定义，则f(z)在区域D内一 点z=x+iy可导的充要条件是 (1) 二元实函数u(x,y)和v(x,y)在点(x,y)可微； (2) u(x,y),v(x,y)在点(x,y)满足柯西-黎曼方程. , . u v u v x y y x     = = −    

例讨论下列函数的性质(1),f(z)= cos(z) ;(2) f(z)=e=e'(cosy+isiny) ;(3),f(z)-Lnz;例 设f(z)=u(x,y)+iv(x,y)=x? + axy+y2 + i(bx2 + 3xy + cy2)求a,b,c

例 讨论下列函数的性质. (1) f(z)= cos(z) ; (2) f(z)=ez=ex (cosy+isiny) ; (3) f(z)=Lnz; 例 设f(z)=u(x,y)+iv(x,y) =x2 + axy+y2 + i(bx2 + 3xy + cy2 ) 求a,b,c

=B积分：( f(2)dz = lim) f(S)Azk20k=l之2定理Zo=A若函数(z)=u(x,y)+iv(x,y)沿曲线C连续，则(z)沿C可积，且[ f(z)dz = [ udx -vdy +i f vdx + udy.cC设C为一光滑或为分段光滑曲线，其参数方程为z=z(t)=x(t)+iy(t)(a≤t<≤b)参数t=a时对应曲线C的起点，t=b时对应曲线C的终点[ f(z)dz= [° f(z(t)z(t)dt.C

积分： 0 1 ( )d lim ( ) , n k k C k f z z f z   → =  =   定理 若函数f(z)=u(x,y)+iv(x,y)沿曲线C连续，则f(z)沿C可积，且 ( )d d d i d d . C C C f z z u x v y v x u y = − + +    设C为一光滑或为分段光滑曲线，其参数方程为 z z t x t y t a t b = = +   ( ) ( ) i ( ) ( ), 参数t=a时对应曲线C的起点，t=b时对应曲线C的终点. ( )d ( ( )) ( )d . b a C f z z f z t z t t =   

定理（柯西-古尔萨定理）若函数(z)是单连通域D内的解析函数，则(z)沿D内任一条闭曲线C的积分为零，即Φ f(z)dz = 0.C定理（柯西积分公式）若(z)是区域D内的解析函数，C为D内的简单闭曲线，C所围内部全含于D内，z为C内部任一点，则Cdc2元i-Z其中积分沿曲线C的正向.上式称为柯西积分公式

定理（柯西-古尔萨定理） 若函数f(z)是单连通域D内的解析函数，则f(z)沿D内任一条闭曲线C 的积分为零，即 ( )d 0. C f z z =  定理（柯西积分公式） 若f(z)是区域D内的解析函数，C为D内的简单闭曲线，C所围 内部全含于D内，z为C内部任一点，则 其中积分沿曲线C的正向.上式称为柯西积分公式. 1 ( ) ( ) d 2π C f f z i z    = − 

定理（高阶导数公式）若（z)为定义在区域D内的解析函数，则在D内其各阶导数都存在并且解析换包句话说，解析函数的导数也是解析函数且有f()d(n =1,2,.:)(S -2)n+(2元1例求复积分1dz =?一a)n

定理（高阶导数公式） 若f(z)为定义在区域D内的解析函数，则在D内其各阶导数都存 在并且解析.换句话说，解析函数的导数也是解析函数. 且有 ( ) 1 ! ( ) ( ) d ( 1,2, ), 2πi ( ) n n C n f f z n z    + = = −  例 求复积分

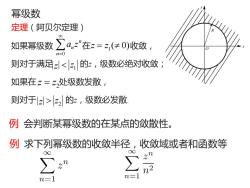
幂级数定理（阿贝尔定理）a,="在z=z(0)收敛,如果幂级数n=0则对于满足z|的z，级数必发散例会判断某幂级数的在某点的敛散性例求下列幂级数的收敛半径，收敛域或者和函数等8nZZ2222n=1n=1

定理（阿贝尔定理） 如果幂级数 在 收敛， 则对于满足 的z，级数必绝对收敛； 如果在 处级数发散， 则对于 的z，级数必发散. 0 n n n a z  =  1 z z = ( 0) 1 z  z 2 z z = 2 z  z 幂级数 例 求下列幂级数的收敛半径，收敛域或者和函数等 例 会判断某幂级数的在某点的敛散性

定理（泰勒定理）设K表示以z.为中心，半径为r的一个圆，f（z)在K内解析，则f（z）可以在K内展开成幂级数，即(Zof(2)=Z(z-zo)n,zeK,n!n=0并称它为,f(z)在z.的泰勒(Taylor)展开式，上式右端的级数称为f(2)的泰勒级数例了解最大模原理的描述

定理 （泰勒定理） 设K表示以z0为中心，半径为r的一个圆， 在K内解析，则 可以在K内展开成幂级数，即 并称它为 在z0的泰勒(Taylor)展开式，上式右端的级数称为 的泰勒级数. f z( ) f z( ) f z( ) f z( ) ( ) 0 0 0 ( ) ( ) ( ) , , ! n n n f z f z z z z K n  = = −   例 了解最大模原理的描述

定理（洛朗定理）设f(z在圆环r<z-zo<R内解析，那么f(2) = Za,(z - z0)",r <|z- zo[<R,f()1其中d5,n = 0,±1,±2,...an+112元i(s-zo)这里C为圆环r<z-zol<R内任何一条绕z的正向简单闭曲线，且f(z)表达式是唯一的例讨论函数1/(z2-3z+2）的孤立奇点，并求在z-2处的洛朗展开。把(z)在z.处的洛朗级数中(z-z)-1项的系数α-,称为(z)在孤立奇点z处的留数，记为 Res[f(z),zo]=α-1;sin z例求在z=0处的留数2

定理（洛朗定理） 设 在圆环 内解析，那么 其中 这里C为圆环 内任何一条绕z0的正向简单闭曲线， 且 表达式是唯一的. f z( ) 0 r z z R  −  0 0 ( ) ( ) , , n n f z a z z r z z R  − = −  −   1 0 1 ( ) d , 0, 1, 2, , 2πi ( ) n n C f a n z    + = =   −  0 r z z R  −  f z( ) 把f(z)在z0处的洛朗级数中(z−z0 ) −1项的系数a−1称为f(z)在孤立奇 点z0处的留数，记为 Res [f(z),z0 ]=a−1 , 例 求 在z=0处的留数 例 讨论函数1/(z2 -3z+2) 的孤立奇点，并求在z=2处的 洛朗展开