《线性代数》课程教学课件（PPT讲稿，A）§3.3 初等矩阵

线性代数 第三章鲜花老三草$ 3.3初等矩阵初等矩阵的概念7、二、初等矩阵的应用三、小结上页下页返回

线性代数 第三章 三、小结 二、初等矩阵的应用 一、初等矩阵的概念 §3.3 初等矩阵 上页 下页 返回

线性代数 第三章第优三车$ 3.3初等矩阵复习矩阵的初等变换初等行变换矩阵的初等变换初等列变换下面三种变换称为矩阵的初等行变换：

线性代数 第三章 复习矩阵的初等变换 §3.3 初等矩阵 下面三种变换称为矩阵的初等行变换: 矩阵的初等变换    初等列变换 初等行变换

线性代数 第三章第样乐花光三堂()对调两行（对调,j两行,记作r;台r）；(②)以数k≠0乘以某一行的所有元素3）把某一行所有元素的k倍加到另一行对应的元素上去（第i行的k倍加到第i行上记作r;+kr)同理可定义矩阵的初等列变换(把“r"换成“c")初等变换的逆变换仍为初等变换且变换类型相同

线性代数 第三章 (1)对调两行（对调i, j两行,记作ri  rj）； (2)以 数 k  0 乘以某一行的所有元素; ( ) . 3 记 作 ） 对应的元素上去（第 行 的 倍加到第 行 上 把某一行所有元素的 倍加到另一行 i krj r j k i k + 同理可定义矩阵的初等列变换 (把“r”换成“c”)． 初等变换的逆变换仍为初等变换, 且变换类型相同．

线性代数 第三章第花老三再复习矩阵等价：如果矩阵A经有限次初等变换变成矩阵B就称矩阵A与B等价，记作A～B

线性代数 第三章 就称矩阵 与 等价，记作 ． 如果矩阵 经有限次初等变换变成矩 阵 ， A B A B A B ~ 再复习 矩阵等价：

线性代数 第三章第花老三一、初等矩阵的概念定义3.3.1由单位矩阵E经过一次初等变换得到的方阵称为初等矩阵?三种初等变换对应着三种初等方阵1.对调两行或两列：2.以数k≠0乘某行或某列3.以数k乘某行（列）加到另一行（列）上去

线性代数 第三章 定义3.3.1 由单位矩阵E 经过一次初等变换得 到的方阵称为初等矩阵. 三种初等变换对应着三种初等方阵.       以数 乘某行（列）加到另一行（列）上去． 以数 乘某行或某列； 对调两行或两列； k k 3. 2. 0 1. 一、初等矩阵的概念

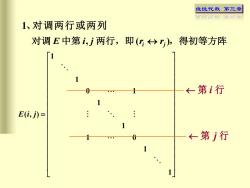
线性代数第三章祥样三堂1、对调两行或两列，得初等方阵对调E中第ii两行，即(r;r)，←第i行E(i,j) =←第i行

线性代数 第三章 对调 E 中第 i, j 两行，即(ri  rj )，得初等方阵 1、对调两行或两列 1 1 0 1 1 ( , ) 1 1 0 1 1 E i j     =    第 i 行  第 j 行

线性代数第三章第优三堂2、以数k±0乘某行或某列以数k≠0乘单位矩阵的第行(r,×k)，得初等矩阵E(i(k))←第i行E(i(k)) =

线性代数 第三章 2 0 、以数 k  乘某行或某列 ( ( )). 0 ( ) E i k k i ri k 矩阵 以数  乘单位矩阵的第 行  ，得初等 1 1 ( ( )) 1 1 E i k k           =              第 i 行

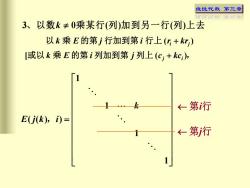
线性代数 第三章第年花老三3、以数k≠0乘某行（列)加到另一行（列)上去以k乘E的第i行加到第i行上（r;+kr,）[或以k乘E的第i列加到第j列上(c;+kc;),←第行E(j(k), i) =←第行

线性代数 第三章 3 0 ( ) ( ) 、以数k  乘某行 列 加到另一行 列 上去 或以 乘 的第 列加到第 列上 ， 以 乘 的第 行加到第 行上 [ ( ) ( ) j i i j k E i j c kc k E j i r kr + + 1 1 ( ( ) ) 1 1 k E j k i           =             ，  第i行  第j行

线性代数 第三章第花老三堂初等矩阵是可逆的，逆矩阵仍为初等矩阵E(i, j)-1 = E(i, j);E(i(k)-1 = E(i(_);kE(j(k),i)-1 = E(j(-k),i) 对矩阵进初等行变换，可以用相应的初等矩阵左乘或右乘矩阵来表示

线性代数 第三章 1 1 1 ( , ) ( , ); 1 ( ( )) ( ( )); ( ( ), ) ( ( ), ) . E i j E i j E i k E i k E j k i E j k i − − − = = = − 对矩阵进初等行变换，可以用相应的初等矩阵 左乘或右乘矩阵来表示. 初等矩阵是可逆的，逆矩阵仍为初等矩阵

线性代数 第三章例祥样三堂001ala12a1a12l100k(1)ka,ka22kazn(2a2n2100(31(3)a3n32a3n11320ka(12a +ka3aliz + kas20(2)(2)a22a2112213)132(31(132byb,00bb,b.b22(3)b21b23b.?-b33b32Db31DD

线性代数 第三章 11 12 21 22 31 32 1 0 (2) 0 1 0 0 0 1 k a a a a a a                11 31 12 32 21 22 31 32 a ka a ka a a a a   + +   =       11 12 13 21 22 23 31 32 33 1 0 0 (3) 0 0 1 0 1 0 b b b b b b b b b                11 13 12 21 23 22 31 33 32 b b b b b b b b b     =       11 12 1 21 22 2 31 32 3 1 0 0 (1) 0 0 0 0 1 nnn a a a k a a a a a a                11 12 1 21 22 2 31 32 3 n nn a a a ka ka ka a a a     =       例