《高等数学》课程教学资源（PPT课件）第五章课件

第五章Advancedmathematics高等数学向量与空间解析几何人民邮电出版社

1 第五 章 向量与空间解析几何 第五章 人民邮电出版社 Advanced mathematics 高等数学 向量与空间解析几何

第五章内容导航第一节向量及其运算第二节平面及其方程第三节直线及其方程第四节曲面与曲线

2 第五 章 向量与空间解析几何 第五章 内容导航 第二节 平面及其方程 第三节 直线及其方程 第四节 曲面与曲线 第一节 向量及其运算

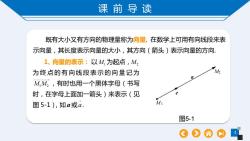
课前导读既有大小又有方向的物理量称为向量．在数学上可用有向线段来表示向量，其长度表示向量的大小，其方向（箭头）表示向量的方向1、向量的表示：以M为起点，MM为终点的有向线段表示的向量记为MM，，有时也用一个黑体字母（书写时，在字母上面加一箭头）来表示（见M1图5-1），如a或a图5-1

课 前 导 读 3 既有大小又有方向的物理量称为向量. 在数学上可用有向线段来表 示向量，其长度表示向量的大小，其方向（箭头）表示向量的方向. 1、向量的表示： 以 M1 为起点， M2 为终点的有向线段表示的向量记 为 M M1 2 ，有时也用一个黑体字 母（书写 时，在字母上面加一箭头）来表示（见 图 5-1），如 a 或a . M1 M2 e a 图5-1

课前导读2、向量的模：向量的大小（数学上有向线段的长度）叫做向量的模，记作al，M,M.模为1的向量称为单位向量，记作e.模为0的向量称为零向量，记作0.零向量的方向可以看作是任意方向3、向径：以原点O为始点，向一点M引向量OM，这个向量叫做点M对于点O的向径，记作r，即r=OM.4自由向量：只与大小、方向有关，而与起点无关的向量称为自由向量

课 前 导 读 4 2、向量的模： 向量的大小（数学上有向线段的长度）叫做向量的 模，记作 a ， M M1 2 .模为1的向量称为单位向量，记作 e . 模为0 的向 量称为零向量，记作0 . 零向量的方向可以看作是任意方向. 3、向径： 以原点O为始点，向一点 M 引向量OM ，这个向量叫 做点M 对于点O的向径，记作r ，即r = OM . 4、自由向量：只与大小、方向有关，而与起点无关的向量称为自 由向量

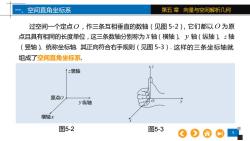
一、空间直角坐标系第五章向量与空间解析几何过空间一个定点O，作三条互相垂直的数轴（见图5-2），它们都以O为原点且具有相同的长度单位，这三条数轴分别称为x轴（横轴）V轴（纵轴）z轴（竖轴）统称坐标轴.其正向符合右手规则（见图5-3）：这样的三条坐标轴就组成了空间直角坐标系1=竖轴原点01y纵轴横轴x图5-2图5-3

5 第五 章 向量与空间解析几何 过空间一个定点O，作三条互相垂直的数轴（见图 5-2）， 一、空间直角坐标系 图5-2 图5-3 原点O z竖轴 y 纵轴 横轴 x O y x z 它们都以 O 为 原 点且具有相同的长度单位，这三条数轴分别称为 x 轴（横轴）、 y 轴（纵轴）、z 轴 （竖轴）、统称坐标轴. 其正向符合右手规则（见图 5-3）. 这样的三条坐标轴就 组成了空间直角坐标系

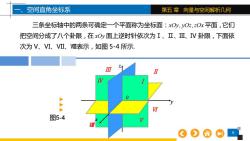
一、空间直角坐标系第五章向量与空间解析几何三条坐标轴中的两条可确定一个平面称为坐标面：xOyyOz,zOx平面，它们把空间分成了八个卦限，在xOv面上逆时针依次为I、Ⅱ、I、IV卦限，下面依次为V、VI、VII、VI表示，如图5-4所示ⅡI1元VI图5-4

6 第五 章 向量与空间解析几何 三条坐标轴中的两条可确定一个平面称为坐标面：xOy yOz zOx , , 平面，它们 把空间分成了八个卦限，在 xOy 面上逆时针依次为Ⅰ、Ⅱ、III、IV 卦限，下面依 次为 V、VI、VII、Ⅷ表示，如图 5-4 所示. 一、空间直角坐标系 图5-4▲▲▲ z y x Ⅲ Ⅱ Ⅳ Ⅰ Ⅴ Ⅵ Ⅷ 0

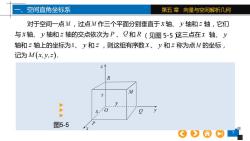
一、空间直角坐标系第五章向量与空间解析几何对于空间一点M，过点M作三个平面分别垂直于x轴、y轴和z轴，它们与x轴、轴和z轴的交点依次为P、Q和R（见图5-5这三点在x轴、J轴和z轴上的坐标为x、y和z则这组有序数x、y和z称为点M的坐标记为 M(x,y,z).RM19图5-5

7 第五 章 向量与空间解析几何 对于空间一点M ，过点M 作三个平面分别垂直于 x 轴、 y 轴和 z 轴，它们 与 x 轴、 y 轴和 z 轴的交点依次为 P 、Q 和 R （见图 5-5）， 图5-5 一、空间直角坐标系 z z x ▲▲▲ y 这三点在 x 轴 、 y 轴和 z 轴上的坐标为x、 y 和 z ，则这组有序数 x 、 y 和 z 称为点M 的坐标， 记为 M x y z ( , , )

一、空间直角坐标系第五章向量与空间解析几何反之，已知一有序数组x、y和z，我们可以在x轴、y轴和z轴上分别取坐标为x的点P，坐标为V的点O，坐标为Z的点R，过三个点分别作垂直于x轴、y轴和z轴的三个平面，它们相交于一点M，这M即为以x、y和z为坐标的点，所以通过直角坐标系，我们建立了空间点M与有序数组X、V和Z的一对应关系，见图5-6RLO8图5-6

8 第五 章 向量与空间解析几何 反之，已知一有序数组 x 、 y 和 z ，我们可以在 x 轴、 y 轴和 z 轴上分别取 坐标为 x 的点 P ，坐标为 y 的点Q ，坐标为 z 的点 R ，过三个点分别作垂直于 x 轴、 y 轴和 z 轴的三个平面，它们相交于一点M ，这M 即为以 x 、 y 和 z 为坐标 的点，所以通过直角坐标系，我们建立了空间点 M 与有序数组 x 、 y 和 z 的一一 对应关系，见图 5-6. 图5-6 一、空间直角坐标系 z y x R P Q M O r

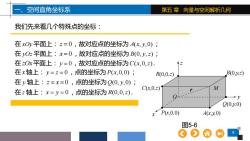
一、空间直角坐标系第五章向量与空间解析几何我们先来看几个特殊点的坐标：在xOy平面上：z=0，故对应点的坐标为A(x,y,0）;在yOz平面上：x=0，故对应点的坐标为B(0,y,z）;在zOx平面上：y=0，故对应点的坐标为C(x,0,2).在x轴上：y=z=0，点的坐标为P(x,0,0）;B(0,,2)R(0.0,2)在y轴上：z=x=0，点的坐标为Q(0,y,0）;MC(x,0,z)在z轴上：x=y=0，点的坐标为R(0,0,z)VQ(0,y,0)P(x,0,0)A(x,y,0)图5-609谷A

9 第五 章 向量与空间解析几何 我们先来看几个特殊点的坐标： 在 xOy 平面上： z = 0，故对应点的坐标为 A x y ( , ,0) ； 在 yOz 平面上： x = 0，故对应点的坐标为 B y z (0, , )； 在 zOx平面上： y = 0，故对应点的坐标为C x z ( ,0, ). 在 x轴上： y z = = 0，点的坐标为 P x( ,0,0) ； 在 y 轴上： z x = = 0 ，点的坐标为Q y (0, ,0) ； 在 z 轴上： x y = = 0，点的坐标为 R z (0,0, ). 图5-6 一、空间直角坐标系 z y x R(0,0,z) C(x,0,z) P(x,0,0) A(x,y,0) Q(0,y,0) B(0,y,z) M O r

一、空间直角坐标系第五章向量与空间解析几何设M(x,J,z）、M(x2,y2,=2)为空间两个点（见图5-7），通过M、M,各作三个分别垂直于三条坐标轴的平面，这六个平面组成一个以M，、M,为对角线的长方体，由此可得d=M,M=V(x2-x）+(y2-)+(z2-z)即d2=M,M=(2 -x)+(y2 -)+(z2 -z) ,M图5-710

10 第五 章 向量与空间解析几何 设 M x y z 1 1 1 1 ( , , )、 M x y z 2 2 2 2 ( , , )为空间两个点（见图 5-7），通过 M1 、M2 各作 三个分别垂直于三条坐标轴的平面，这六个平面组成一个以 M1 、M2 为对角线的长 方体， ( ) ( ) ( ) 2 2 2 2 2 1 2 2 1 2 1 2 1 即 d M M x x y y z z = = − + − + − ， 由此可得 ( ) ( ) ( ) 2 2 2 1 2 2 1 2 1 2 1 d M M x x y y z z = = − + − + − . 图5-7 一、空间直角坐标系 ▲▲▲ z z2 y1 y2 y x M 1 M2 z1 x2 x1 O