《线性代数》课程教学课件（PPT讲稿，A）第四章 线性方程组 §4.1 线性方程组的解的判别

线性代数 第四章祥祥花光国第四章线性方程组S 4.1 线性方程组的解的判别S 4.2 齐次线性方程组的解的结构84.3非齐次线性方程组解的结构

线性代数 第四章 第四章 线性方程组 §4.2 齐次线性方程组的解的结构 §4.1 线性方程组的解的判别 §4.3 非齐次线性方程组解的结构

线性代数 第四章美品章84.1线性方程组的解的判别auxi +aix, +...+anx, =bn元a21Xi +a22x, +...+a2nx, =b,线性(4-1)方程组amiX+am2X2+...+amXn=bbala12aainay2an记ban2a21anna21a22aznA=A=baaaamlam2amlm2mmnmn增广矩阵系数矩阵

线性代数 第四章 n 元 线性 方程组 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (4 1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =  −    + + + = 11 12 1 21 22 2 1 2 , n n m m mn a a a a a a A a a a       =       记 §4.1 线性方程组的解的判别 系数矩阵 增广矩阵 11 12 1 1 21 22 2 2 1 2 n n m m mn m a a a b a a a b A a a a b       =      

线性代数 第四章祥彩光国堂aiixi+ax,+...+anx, =ba2ix+a22x2+...+a2nx,=b,(4 -1)amX, +am2X, +...+amnX, = b,mbXiana2ainbX2a21a122a2n记 A=b=，x=....bamlaaXnm2mnm则，非齐次方程组（4-1）可以记为：Ax=b（4-2）

线性代数 第四章 1 1 2 2 , . n m x b x b x b x b             = =             则，非齐次方程组（4-1）可以记为：Ax = b（4-2） 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (4 1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =  −    + + + = 11 12 1 21 22 2 1 2 , n n m m mn a a a a a a A a a a       =       记

线性代数 第四章手发光国临由第二章的讨论可知，方程组(4-1)与增广矩阵A具有一一对应关系，对方程组进行加减消元相当于对其增广矩阵进行初等变换，因此求解方程组的问题就可以转化为矩阵的初等行变化的问题一般线性方程组的解可能会出现三种情况：1.有唯一解;2.有无穷多解；3.无解

线性代数 第四章 由第二章的讨论可知，方程组(4-1)与增广矩阵A 具有一一对应关系，对方程组进行加减消元相当于对 其增广矩阵进行初等变换，因此求解方程组的问题 就可以转化为矩阵的初等行变化的问题. 一般线性方程组的解可能会出现三种情况： 1. 有唯一解； 2. 有无穷多解； 3. 无解

线性代数 第四章祥祥花光国一、线性方程组解的判别线性方程组：定理4.1.1anxi +ax +...+ainx,=ba21xj+a22+.+a2nx,=b,(4-1)am,+am2X+...+amx,=bm有解的充分必要条件是它的系数矩阵A与增广矩阵A有相同的秩即R(A) = R(A)

线性代数 第四章 一、线性方程组解的判别 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 4.1.1 (4 1) , ( ) ( ). n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b A A R A R A  + + + =   + + + =  −   + + + =  = 线性方程组： 有解的充分必要条件是它的系数矩阵 与增广矩阵 有相同的秩 即 定理

线性代数 第四章祥彩光品堂证：对于一般线性方程组aux +a2x, +...+anx, =ba2ixi+a22x2+...+a2nxn=b(4-1)[amiX, +amX, +...+amnx,=b,mbania12ainb,a22a2)aan设α=,β=,αz =,αnba.aamlm2mnm

线性代数 第四章 证： 对于一般线性方程组 11 12 1 1 21 22 2 2 1 2 1 2 , , , , n n n m m mn m a a a b a a a b a a a b                             = = = =                             11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (4 1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =   + + + =  −   + + + =  设

线性代数第四章鲜装品堂则线性方程组（4-1）可写为(4-3)Xαi +x,α, +...+xnαn =β并且A-[α α, ... αn]A-[α α, ... α, β]必要性若方程组有解，则由(4-3)知β可由αi,α2,.…,α,线性表示，于是向量组α,α……,α,与向量组α,α2……αβ等价由性质2.3.1知秩（α,α..,α,}=秩α,α2....αβ)，所以R(A) = R(A)

线性代数 第四章 则线性方程组（4-1）可写为 1 1 2 2 (4 3) n n x x x     + ++ = − 1 2 1 2 n n A A        =      =      并且 1 2 1 2 1 2 1 2 1 2 (4 3) , , , , , , , , , , . 2.3.1 , , , , , , ( ) ( ). n n n n n R A R A                   −      = 若方程组有解，则由 知 可由 线性 表示，于是向量组 与向量组 等价由性质 知秩{ }=秩{ , }, 所以 必要性

线性代数第四章花品充分性若R(A)= R(A),则向量组α,α2,……,α,与向量组α,α2,……,αn,β有相同的秩，所以向量组α,α2,……,α,的最大无关组一定是α,αz,…,αn，β的最大无关组，因此β可由向量组αi,α2..……,α,线性表示.由(4-3)知方程组(4-1)有解x,α, +x,α, +...+x,αn=β (4-3)aiXi +ai2X2 +...+ainxn =ba21Xj +a22X, +...+a2nXn = b,(4-1)amiXi+am2X2 +...+ammX,=bmn1m

线性代数 第四章 充分性 1 2 1 2 1 2 1 2 1 2 ( ) ( ) , , , , , , , , , , , , , , , , . (4 3) (4 1) . n n n n n R A R A                   =      − − 若 ，则 向 量 组 与 向 量 组 有 相 同 的 秩，所 以 向 量 组 的 最 大 无 关 组 一 定 是 , 的 最 大 无 关 组，因 此 可 由 向 量 组 线 性 表 示 由 知 方 程 组 有 解 1 1 2 2 (4 3) n n x x x     + ++ = − 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 (4 1) n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b  + + + =  + + + =  −  + + + =

线性代数 第四章祥祥花光国推论1当R(A)± R(A)时，方程组(4-1)无解推论2如果方程组(4-1)有解，则它有惟一解的充分必要条件是R(A)=R(A)= n.推论3 如果方程组(4-1)有解，且R(A)= R(A)< n,则方程组(4-1)有无穷多解X -2x, +3x -x =1,例1判断方程组3x,-x,+5x,-3x=2,是否有解2x, +X, +2x3-2x =3

线性代数 第四章 3 (4 1) ( ) ( ) , (4 1) . − =  R A R A n − 如果方程组 有解，且 则方程组 有 推 无穷多解 论 推 论1 ( ) ( ) (4 1 当 R A R A  − 时 ， 方 程 组 ) . 无 解 1 2 3 4 1 2 3 4 1 2 3 4 2 3 1, 1 3 5 3 2, . 2 2 2 3 x x x x x x x x x x x x  − + − =   − + − =  + + − =  例 判断方程组 是否有解 (4 1) ( ) ( ) . 2 R A R A n − = = 如果方程组 有解，则它有惟一解的 充分必要条件是 推论

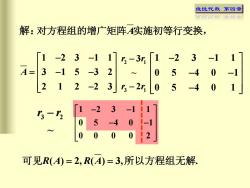
线性代数第四章祥祥花光国解：对方程组的增广矩阵A实施初等行变换3rA=32322rO1-23r3-r205-400000可见R(A)= 2,R(A)= 3,所以方程组无解

线性代数 第四章 1 2 3 1 1 3 1 5 3 2 2 1 2 2 3 A   − −   = − −       − 2 1 3 1 3~2 r r r r −− 1 2 3 1 1 0 5 4 0 1 0 5 4 0 1   − −   − −       − 3 2 ~ r r − 1 2 3 1 1 0 5 4 0 1 0 0 0 0 2   − −   − −       解： 对方程组 的 增 广矩 阵 A实施初等行变换， 可见R A R A ( ) 2, ( ) 3, . = = 所以方程组无解