《线性代数》课程教学课件（PPT讲稿，A）§2.4 矩阵的秩

线性代数 第二章新乐我桃川科$ 2.4矩阵的秩矩阵的行(列)秩、秩矩阵秩的求法二、三、向量组的秩、最大无关组的求法四、k阶子式五、小结上页下页返回

线性代数 第二章 §2.4 矩阵的秩 一、 矩阵的行(列)秩、秩 二、 矩阵秩的求法 三、向量组的秩、最大无关组 的求法 四、 k 阶子式 五、小结 上页 下页 返回

线性代数 第二章我新乐我就科一、矩阵的行(列)秩、秩定义2.4.1设mXn矩阵A，称A的行向量组的秩为矩阵A的行秩，列向量组的秩称为矩阵A的列秩0例1求矩阵A=的行秩和列秩01224解： A的行向量α, =(1,0,1),α, =(0,1,2),α, =(2,1,4)由行列式012=0，知向量组αi,αz,α,线性相关,42

线性代数 第二章 定义2.4.1 设m×n矩阵A，称A 的行向量组的秩为矩阵A的 行秩，列向量组的秩称为矩阵A的列秩. 一、矩阵的行(列)秩、秩 1 0 1 1 0 1 2 . 2 1 4 A     =       例 求矩阵 的行秩和列秩 1 2 3 A的行向量   = = = (1,0,1), (0,1,2), (2,1,4) 1 2 3 1 0 1 0 1 2 0 , , 2 1 4 由行列式 = ，知向量组   线性相关， 解：

线性代数 第二章我新乐装然川科又α,α,线性无关，故α,α,是A的行向量组的一个最大无关组，所以矩阵A的行秩等于2.同样方法可以求出A的列秩等于2１3例2求矩阵A=-1的行秩和列秩，0275000解： A的行向量α, =(1,1,3,1),α, =(0,2,-1,4),αg = (0,0,0,5)去掉第三个分量，得α, =(1,1,1),α, = (0,2,4),α, = (0,0,5)

线性代数 第二章 1 2 1 2 , , 2. A A 又    线性无关，故 是 的行向量组的一个 最大无关组，所以矩阵 的行秩等于 1 2 3 (1,1,3,1), (0,2, 1,4), (0,0,0,5). A    = = − = 的行向量 同样方法可以求出A的列秩等于2. 1 1 3 1 2 0 2 1 4 . 0 0 0 5 A     = −       例 求矩阵 的行秩和列秩 解： 1 2 3       = = = (1,1,1), (0,2,4), (0,0,5). 去掉第三个分量，得

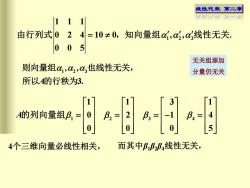
线性代数 第二章教新乐教二料1由行列式0知向量组α,α,α线性无关，24=10±0，500无关组添加则向量组α,α,,α,也线性无关分量仍无关所以A的行秩为3.[131142A的列向量组β,=β, =|-10β, =β=[o][5][o]0而其中βββ4线性无关，4个三维向量必线性相关

线性代数 第二章 1 2 3 111 0 2 4 10 0 , , 005 由行列式 =  ，知向量组     线性无关. 1 2 3 , , A 3. 则向量组   也线性无关， 所以 的行秩为 1 2 3 4 1 1 3 1 0 2 1 4 0 0 0 5 A                     = = = − =                         的列向量组 4个三维向量必线性相关， 而其中β1β2β4线性无关， 无关组添加 分量仍无关

线性代数 第二章我新我桃科00因为10=10±055所以A的列秩也等于3例1和例2中矩阵的行秩等于列秩并非是偶然的。为了证明这一点，我们有以下两个定理定理2.4.1初等行(列)变换不改变矩阵的行(列)秩证明略

线性代数 第二章 1 0 0 1 2 0 10 0 1 4 5 =  因为 所以A的列秩也等于3. 例1和例2中矩阵的行秩等于列秩并非是偶然的. 为了证明这一点，我们有以下两个定理. 定理2.4.1 初等行(列)变换不改变矩阵的行(列)秩. 证明： 此处只就第三种初等行变换不改变矩阵的 行秩证明之，其余两种课下自己来完成 证明略.

线性代数 第二章 1 2 , , 设m n A  矩阵 的行向量组   ， m ，且 1 1 ~ i j i j i r kr j j m m k A B          +                   +     = =                            

线性代数 第二章 1 1 ( ) i i j j m m k k         = = + − = 由 可知，矩阵A的行向量组可由B的行向量组线性表示. 显然，矩阵B的行向量组可由A的行向量组线性 表示.所以，矩阵A、B的行向量组等价.从而矩阵A、 B的行向量组的秩相同

线性代数 第二章张二本定理2.4.1亦可作为初等变换不改变线性方程组中独立方程的个数的理论依据定理2.4.2初等行(列)变换不改变矩阵列(行)向量间的线性关系.03例3设矩阵A=其列向量-1526042αr,αz,αg,α,间有线性关系：α, =α, +2α,-αg,矩阵矩阵A经过有限次初等行变换得到验证B的列向量β,βz,β3,β,间也有线性关系β =β,+2βz -β3

线性代数 第二章 定理2.4.1亦可作为初等变换不改变线性方程组中 独立方程的个数的理论依据 定理2.4.2 初等行(列)变换不改变矩阵列(行)向量间的 线性关系. 1 2 3 4 4 1 2 3 1 2 3 4 4 1 2 3 1 1 3 0 3 0 2 1 5 6 0 2 4 , , , 2 . , 2 A B A B                     = −       = + − = + − 例 设矩阵 其列向量 间有线性关系： ， 矩阵 由矩阵 经过有限次初等行变换得到 验证 的列向量 间也有线性关系

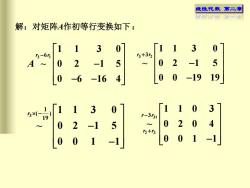
线性代数 第二章师乐光二解：对矩阵A作初等行变换如下：0013+3r2r3-6ri50252419-1900-164-603Xr-3r31152+r3000

线性代数 第二章 解：对矩阵A作初等行变换如下： 3 1 6 1 1 3 0 ~ 0 2 1 5 0 6 16 4 r r A −     −       − − 3 2 3 1 1 3 0 ~ 0 2 1 5 0 0 19 19 r r +     −       − 3 1 ( ) 19 1 1 3 0 ~ 0 2 1 5 0 0 1 1 r  −     −       − 31 2 3 3 1 1 0 3 ~ 0 2 0 4 0 0 1 1 r r r r − +           −

线性代数 第二章教南乐装城川料013ri-r220=B12容易看出，B的列向量β,β,,β,β间也有线性关系β=β,+2β,-β3实际上，如果把以上每作一次初等行变换所得到的矩阵叫做B的话,B的列向量间同样存在上述线性关系推论初等行(列)变换不改变矩阵的列(行)秩

线性代数 第二章 2 1 2 1 1 0 3 ~ 0 1 0 2 0 0 1 1 r            − 1 2 1 0 0 1 ~ 0 1 0 2 0 0 1 1 r r B −     =       − 1 2 3 4 4 1 2 3 , 2 . B         = + − 容易看出， 的列向量 间也有 线性关系 实际上，如果把以上每作一次初等行变换所得到的 矩阵叫做B的话,B的列向量间同样存在上述线性关系. 推论 初等行(列)变换不改变矩阵的列(行)秩