《复变函数与积分变换》课程教学课件（PPT讲稿）第二章 解析函数

第二章解析函数2.1复变函数2.2导数与解析函数2.3初等函数

第二章 解析函数 2.1 复变函数 2.2 导数与解析函数 2.3 初等函数

S 2. 1 复变函数复变函数的基本概念复变函数的极限复变函数的连续

* ◼ 复变函数的基本概念 ◼ 复变函数的极限 ◼ 复变函数的连续 §2.1 复变函数

82.1.1复变函数的基本概念定义2.1设E为一复数集.若对E中的每一个复数z=x+iy按照某种法则有确定的一个或几个复数w=u+iv与之对应，那么称是定义E上的复变数的函数（简称复变函数），记作W=f(E称为定义域，E中所有的对应的一切w值构成的集合称为的值域，记作E).f(E)={WEzEE,f(z)=W)12Rez ImzznargzArgz

§2.1.1 复变函数的基本概念 定义2.1 设E为一复数集.若对E中的每一个复数 ,按照某种法则f有确定的一个或几个复数 与之 对应，那么称f是定义E上的复变数z的函数（简称复变 函数），记作 . z x y = + i w u v = +i w f z = ( ) f E w z E f z w ( ) { | , ( ) } =   = E称为定义域. E中所有的z对应的一切w值构成的集合称 为f的值域，记作 f(E)

例函数W=z令z=x+iy,w=u+iv,则 u+iv =(x+iy)?=x?- y? +2xyi,于是函数w=z对应于两个二元实变函数：u=x?-y2, v=2xy.它们确定了自变量为和√的两个二元实变函数

例 , 2 函数w = z 令 z = x + iy, w = u + iv, 2 则 u + iv = (x + iy) 2 , 2 2 = x − y + xyi : 于是函数 w = z2 对应于两个二元实变函数 , 2 2 u = x − y v = 2xy. 它们确定了自变量为x 和 y的两个二元实变函数. 4

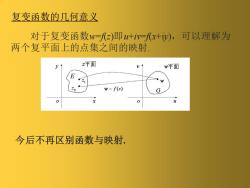
复变函数的几何意义对于复变函数w=/=)即u+iv=(x+iy)，可以理解为两个复平面上的点集之间的映射2平面w平面EZ1WW= f(z)Z+x0u.今后不再区别函数与映射

对于复变函数w=f(z)即u+iv=f(x+iy)，可以理解为 两个复平面上的点集之间的映射. 复变函数的几何意义 今后不再区别函数与映射

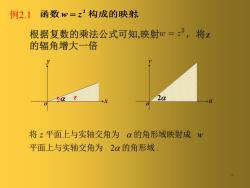
函数W=z?构成的映射例2.1根据复数的乘法公式可知，映射W=，将z的辐角增大一倍+X将z平面上与实轴交角为为α的角形域映射成w平面上与实轴交角为2α的角形域

. 函数 w = z 2 构成的映射  2 6 例2.1 根据复数的乘法公式可知,映射 ，将z 的辐角增大一倍 2 . 平面上与实轴交角为 的角形域 将 平面上与实轴交角为 的角形域映射成  z  w

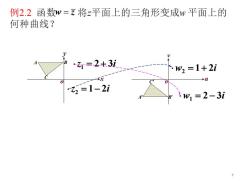
例2.2函数w=z将z平面上的三角形变成w平面上的何种曲线？=2±3i·W, =1+2i+l=1-2iwi =2-3i

z 2 3i  1 = + w 2 3i  1 = − z 1 2i  2 = − w 1 2i  2 = + A B C A B C 7 例2.2 函数 w z = 将z平面上的三角形变成w 平面上的 何种曲线？

例2.3函数W==将z平面上的直线x=1变成w平面上2的何种曲线？￥1x-iy解: z=x+iy,w=u+iv= x? + y2x+iyZz平面上的直线x=1对应于w平面上的曲线1yuV1+ y1+ y1u(1+ y)2(1+y)?1=uyt之平面U1+ yw平面cu04=ltC

例2.3 函数 将z平面上的直线x=1变成w 平面上 的何种曲线？ 1 w z = 解： 2 2 1 1 i i , i i x y z x y w u v z x y x y − = + = + = = = + + z平面上的直线x=1对应于w平面上的曲线 2 2 1 , 1 1 y u v y y = = − + + 2 2 2 2 2 2 2 2 1 (1 ) (1 ) 1 1 y u v y y u y + = + + + = = + 1 1 2 2 ( ) 2 4 u v − + =

反函数的定义设W=f（z的定义集合为z平面上的集合E,函数值集合为W平面上的集合F=fE),那末F中的每一个点W必将对应着E中的一个或几个点。于是在F上就确定了一个单值或多值)函数,记作：z=f-l(w),它称为函数w=f(z)的反函数,也称为映射W=f(z)的逆映射如果函数(映射)W=f(z)与它的反函数(逆映射)z =Φ(W)都是单值的那末称函数(映射)W=f(z)是一一对应的也可称集合E与集合F是一一对应的

反函数的定义 ( ) . ( ), ( ) , 每一个点 必将对应着 中的一个 或几个 点 数值集合为 平面上的集合 那 末 中 的 设 的定义集合为 平面上的集合 函 w E w F f E F w f z z E = = ( ) . ( ), ( ) , ( ) , 1 为映射 的逆映射 它称为函数 的反函数 也 称 于是在 上就确定了一个单值或多值 函 数 w f z z f w w f z F = = = − 记作： 9 . ) ( ) . ( ) ( ) , ( ( ) ( ) 合 是一一对应的 射 是一一对应的也可称集合 与 集 逆映射 都是单值的那末称函数 映 如果函数 映 射 与它的反函数 F w f z E z w w f z = = = 

$ 2.1.2复变函数的极限定义2.2设函数w=(z)定义在z.的去心邻域0z.时的极限存在，常数A为其极限值记作lim f(z) = AZ>20或 f(2) → A(z →z).以我为心，心中无我虚怀若谷，放眼苍穹

§2.1.2 复变函数的极限 定义2.2 设函数w=f(z)定义在z0的去心邻域0<|z-z0 |<r内， 若存在常数A，对于任意给定<0的,都存在一正数 (0<r),使得当0<|z-z0 |< r时,有 , 则称函数f(z)当z→z0时的极限存在，常数A为其极限值. 记作 或 . f z A ( ) −   0 lim ( ) z z f z A → = 0 f z A z z ( ) ( ) → → 以我为心，心中无我 虚怀若谷，放眼苍穹