《线性代数》课程教学课件（PPT讲稿，A）§3.4 分块矩阵

线性代数 第三章第三车$ 3.4分块矩阵一、分块矩阵的概念二、分块矩阵的运算三、分块对角矩阵

线性代数 第三章 一、分块矩阵的概念 二、分块矩阵的运算 三、分块对角矩阵 §3.4 分块矩阵

线性代数第三章00001祥样三草0200130020如A=，求[A|及A-1。0030-100204AlA=V22A33

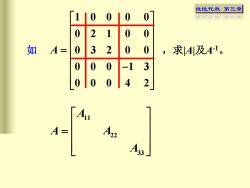
线性代数 第三章 如 11 22 33 A A A A     =       1 0 0 0 0 0 2 1 0 0 0 3 2 0 0 0 0 0 1 3 0 0 0 4 2 A       =     −       ，求|A|及A-1

线性代数第三章花三一、分块矩阵的概念定义设A是一个矩阵，在A的行或列之间加上一些线，把这个矩阵分成若干小块：用这种方法被分成若干小块的矩阵叫做一个分块矩阵.每一小块称为A的子块，每一个分块的方法叫做A一种分法ala12a13ay115则A可记作a22123aa2)2524例如 A=AA2A3A=(13)a32a34a33135A23AA22A54a42a43a44

线性代数 第三章 一、分块矩阵的概念 定义 设A是一个矩阵，在A的行或列之间加上一些 线，把这个矩阵分成若干小块．用这种方法被分成 若干小块的矩阵叫做一个分块矩阵.每一小块称为A 的子块，每一个分块的方法叫做A一种分法. 例如 31 32 3 11 3 13 14 23 24 1 41 42 5 25 34 43 4 12 2 35 1 4 5 22 4 a a a a a a a a a a a a a a a a a a a A a       =       则A可记作 21 1 12 3 1 2 2 13 A 2 A A A A A   A =    

线性代数第三章祥彩光三草000A1例: A=其中=BEb一1a0i0=(A A, A, A),其中A=A=b0b

线性代数 第三章 ,  = E B A O ( ), = A1 A2 A3 A4   = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0   = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0   = a a A 0 1 其 中   = b b B 1 1   = 0 1 1 0 E   = 0 0 0 0 O   = 010 1 a 其中 A   = 101 2 a A   = 100 3 b A   = b A 100 4 例：

线性代数第三章祥样三草323248856567而：-3-2-3-1-1-24-4-6?-8-7-7-6?不是分块矩阵

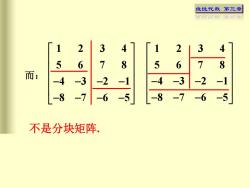
线性代数 第三章 1 2 3 4 5 6 7 8 4 3 2 1 8 7 6 5         − − − −     − − − − 1 2 3 4 5 6 7 8 4 3 2 1 8 7 6 5         − − − −     − − − − 而： 不是分块矩阵

线性代数第三章祥彩光三堂特殊分法设矩阵A=(a,)sxnAA按行分块其中 A, =(ai,ai2,,ain),A=：..i=1,2,...,s.Aajazj按列分块 A=(A,A,",An)，其中A,=j =1,2,...,n.1nj

线性代数 第三章 特殊分法 设矩阵 ( ) , A a = ij s n 按列分块 A A A A = ( 1 2 , , , n ) ，其中 1 2 , j j j nj a a A a       =         j n = 1,2, , . 按行分块 1 2 , s A A A A     =         其中 1 2 ( , , , ), A a a a i i i in = i s = 1,2, ,

线性代数第三章二、分块矩阵的运算祥样花老三1、加法设A，B是两个mXn矩阵，对它们用同样的分法分块：BuBiA1AB=A=BBApIqq其中A,与B,的行数相同列数相同那末+BAu + BA9A+B=+B+B4PInpqq

线性代数 第三章 其中Aij与Bij的行数相同,列数相同,那末 11 11 1 1 1 1 . q q p p pq pq A B A B A B A B A B   + +   + =     + +   11 1 11 1 1 1 , q q p pq p pq A A B B A B A A B B         = =             二、分块矩阵的运算 1、加法 设 A, B 是两个m×n 矩阵，对它们用同样的分法分块:

线性代数第三章祥花光三草2、数量乘法Au.Ala设分块矩阵A=2是任意数，则AAnpqAu2AL2A=2A2Aplq

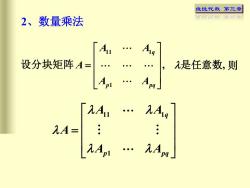
线性代数 第三章 2、数量乘法 设分块矩阵 11 1 1 , , q p pq A A A A A      =       是任意数 则 11 1 1 q p pq A A A A A          =      

线性代数第三章3、乘法祥彩光三堂把矩阵A=（aik）mxs,B=（bj）sxp分块成B1lBadAABBBt1tq其中A,A2,…,A,的列数分别等于B,,B2j,B,的行数,那未CAB=Cp1Cpq其中C, =ZAB(i= 1,..., p;j=1,...,q)

线性代数 第三章 11 1 11 1 1 1 1 2 1 2 , , , , , , , , , t q p pt t tq i i it j j tj A A B B A B A A B B A A A B B B         = =             其 中 的 列 数 分 别 等 于 的 行 数 那 末 ( ) 11 1 1 1 1, , ; 1, , . q p pq t ij ik kj k C C AB C C C A B i p j q =     =       其 中 = = =  3、乘法 把矩阵 ( ) , ( ) A a B b = = ik m s kj s p   分块成

线性代数 第三章三4、转置AuAuA124:A22A2则设分块矩阵A="AAp2Apt4A21AplA'2Ap2.A'=.4-:AptAt

线性代数 第三章 11 21 1 12 22 2 1 2 . p p t t pt A A A A A A A A A A              =            设分块矩阵 11 12 1 21 22 2 1 2 , t t p p pt A A A A A A A A A A       =       则 4、转置