《高等数学》课程教学资源（课件讲稿）第五章课件_第二次课

第一节II向量及其线性运算

第一节II 向量及其线性运算

两向量的数量积一

一、两向量的数量积

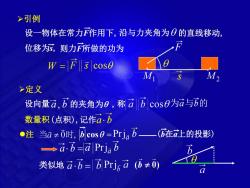
>引例设一物体在常力F作用下，沿与力夹角为①的直线移动F位移为S，！则力F所做的功为0W =|F|3|cos0MiM2S>定义设向量a,b的夹角为e，称ablcoso为a与b的数量积（点积），记作a.b·注 当a→0时,lblcos=Prj,b——(在a上的投影)→a.b=a|Prja b6类似地a.b=bPrjra(b0)C

M1 W   定义 F s cos  M2 a b 设向量 的夹角为 ,称 数量积(点积),记作 a , b 为a与b的 s 引例 设一物体在常力F作用下, 沿与力夹角为 的直线移动, 位移为s, 则力F所做的功为  注 ba  Prj a b  a ba  Prj ( 0)   类似地 b  (b在a上的投影)

>性质() aa=al(2）,b为两个非零向量，则有a.b=0→alb>运算律6a.b-b.a(1)交换律C(,μ为实数）(2)结合律a+b(aa).b=a.(ab)= a(a.b)C(aa)·(ub) =aμ(a.b)Prj.a Prjeb(a+b).=a.+b.c(3)分配律Prj.(a+b)例1证明三角形余弦定理c2=α2+b2-2abcosQ

性质 为两个非零向量, 则有 (1) a  a  (2) a ,b a b  0  运算律 (1)交换律 (2)结合律 a ( b) ( a )( b )    (a b) (3)分配律 c a b  b a bc  a Prj c  Prj Prj (a b) c   例1 证明三角形余弦定理 2 cos . 2 2 2 c  a  b  ab 

>数量积的坐标表示设a=axi+a,j+a,k,b=b,i+b,j+b,ka.b=(a,i+a, j+a, k).(b,i+b, j+b,k).i=.j=k=l,7.j=j.k=k.i=0a.b=axbx +a,b, +a,b当a，b为非零向量时，?.b=|ab|cosa,bx+a,by+a,ba·bcOs =-[ai/6]a+a+a?b+b,+b两向量夹角公式

数量积的坐标表示 设  0 x x y y z z  a b  a b  a b 当 为非零向量时, cos   x x y y z z a b  a b  a b 2 2 2 x y z a  a  a 2 2 2 x y z b  b  b a b cos a a i a j a k ,  x  y  z b b i b j b k ,  x  y  z ( a i  a j  a k ) x y z (b i b j b k ) x  y  z i  j  j  k  k i a b a b 两向量夹角公式

例2已知三点M(1,1,1), A(2,2,1),B(2,1,2),求AMBBM例3设均匀流速为√的流体流过一个面积为A的平面域，且与该平面域的单位垂直向量n的夹角为0,求单位时间内流过该平面域的流体的质量P（流体密度为p）A

例2 B M A M (1,1,1), A( 2, 2,1), B( 2,1 , 2), 求 AMB . 已知三点 例3  A 求单位时间内流过该平面域的 设均匀流速为 的流体流过一个面积为A的 平面域 , 与该平面域的单位垂直向量 的夹角为 且 流体的质量P(流体密度为)

两向量的向量积二

二、两向量的向量积

>引例设0为杠杆L的支点，有一个与杠杆夹角为θ的力F作用在杠杆的P点上，则力F作用在杠杆上的力矩为：M|=|OQF|=|OPF sin0MIOPOPTMIFH0MM的方向符合右手规则o|=|oP|sine

设O为杠杆L 的支点,有一个与杠杆夹角为 OQ  O P L   Q 的方向符合右手规则  OQ F  OP F sin OP sin M M  OP M 作用在杠杆的P点上,则力F作用在杠杆上的力矩为: F o P F M M  F 引例 的力F

>定义设α,b的夹角为,定义方向：a，b且符合右手规则a向量℃模：|=a|sin=axb称为向量a与b的向量积,记作c=α×b(又积)注力矩 M=OP×F

定义 向量 方向: 记作 (叉积) 且符合右手规则 模: 设 a , b的夹角为， c c  a , c  b c  a b sin b a c 称 c 为向量 a 与b 的 向量积, c  a  b  a  b 力矩 定义 注

>性质(l)axa=0(2)a,b为非零向量，xb=→a/>运算律(1)axb =-bxa(a+b)xc=axc+bxc(2)分配律(aa)xb=ax(ab)=a(axb)(3)结合律

性质 (1) a  a  0 (2) a , b 为非零向量, a  b  0 a ∥ b 运算律 (2) 分配律 (3) 结合律  b a ( a  b ) c  a  c  b  c ( a ) b  a  ( b )   ( a b ) (1) a b