《高等数学》课程教学资源（PPT课件）第四章课件_4-1 基本概念 4-2 可分离变量方程4-3齐次方程

7.1微分方程的基本概念7.2可分离变量的微分方程7.3齐次方程

7.1微分方程的基本概念 7.2可分离变量的微分方程 7.3齐次方程

微分方程的基本概念引言(一)(二)基本概念

一 微分方程的基本概念 （一）引言 （二）基本概念

微分方程的基本概念一引言(一)(二)基本概念

一 微分方程的基本概念 （一）引言 （二）基本概念

函数实际问题变量间的联系求解含有未知函数微分方程及其导数的等式例1一曲线通过点（1,2），在该曲线上任意点M(xV）处的切线的斜率为2x，求该曲线的方程例2某列车在平直线路上以20m/s的速度行驶，制动时列车获得加速度a=-0.4m/s，问开始制动后多长时间列车才能停住以及列车在这段时间里行驶了多少路程？

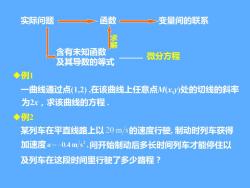
实际问题 函数 变量间的联系 含有未知函数 及其导数的等式 求 解 微分方程 ◆例1 一曲线通过点(1,2) ,在该曲线上任意点M(x,y)处的切线的斜率 为2x，求该曲线的方程 . ◆例2 问开始制动后多长时间列车才能停住以 某列车在平直线路上以 的速度行驶, 制动时列车获得 加速度 及列车在这段时间里行驶了多少路程？

微分方程的基本概念一引言(一)(二)基本概念

一 微分方程的基本概念 （一）引言 （二）基本概念

微分方程的基本概念一引言()二)基本概念

一 微分方程的基本概念 （一）引言 （二）基本概念

微分方程含有未知函数及其导数的方程一元函数常微分方程未知函数多元函数偏微分方程>微分方程的阶方程中所含未知函数导数的最高阶数例：xy"+xy"-4xy=3x三阶微分方程y(4).-4y"-12y+5y= sin2x四阶微分方程一般地F(x,y,y,.",y(n))=0n阶微分方程·注在n阶微分方程中"的系数不为零，其余项的系数可以为零

常微分方程 偏微分方程 含有未知函数及其导数的方程 方程中所含未知函数导数的最高阶数 ( , , , , ) 0 ( )  = n 一般地 F x y y  y ➢微分方程 未知函数 一元函数 多元函数 ➢微分方程的阶 例: 3 2 2 x y x y xy x    + − = 4 3 三阶微分方程 (4) y y y y x − − + = 4 12 5 sin 2   四阶微分方程 n阶微分方程 ⚫注 在n阶微分方程中 ( ) n y 的系数不为零,其余项的系数可以为零

微分方程的解使方程成为恒等式的函数通解解中所含独立任意常数的个数与方程的阶数相同特解不含任意常数的解>定解条件确定通解中任意常数的条件n阶方程的初始条件（或初值条件）(n-l)(xo)= yo , J'(xo) = y , ., J(n-I)(xo) = yo引例2引例1d?ydy=2x=-0.4dxdx24-0 =20Ix=1= 2定解条件V=x+C通s解0.2t-+Ct+Cy=x2+1特S解0.2t-+20t

0 , s t=0 = 20 d 0 d = t t= s 引例2 0.4 2 2 d d = − x y 使方程成为恒等式的函数. 通解 解中所含独立任意常数的个数与方程的阶数相同. ( 1) 0 0 ( 1) 0 0 0 0 ( ) , ( ) , , ( ) − − =  =  = n n y x y y x y  y x y 确定通解中任意常数的条件. n 阶方程的初始条件(或初值条件): 特解 x x y 2 d d = 2 y x=1= 引例1 y = x + C 2 1 2 2 通 s = 解−0.2t +C t +C s 0.2t 20t 2 1 = − + 2 y = x + 特 解 不含任意常数的解。 ➢定解条件 ➢微分方程的解 定 解 条 件

验证函数x=Cicoskt+C2sinktCiC为常数例3d2X是微分方程+k2x=0 的解,并求满足初始条件dtdxt=0=0 的特解,t=0 =At

◆例3 验证函数 是微分方程 的解, , x t=0 = A 0 d 0 d = t t = x 的特解 . 并求满足初始条件 C1，C2为常数

可分离变量的微分方程(一)类型与解法(二)举例

二 可分离变量的微分方程 （一）类型与解法 （二）举例