《高等数学》课程教学资源（PPT课件）第六章课件_6.4复合求导

第八章第四节多元复合函数的求导法则一元复合函数y=f(u), u=@(x)dydy du求导法则dxdu dx微分法则dy= f(u)du=f(u)p'(x)dx本节内容：多元复合函数求导的链式法则一、二、多元复合函数的全微分HIGHEDUCATIONPRESS机动目录下页返回结束上页

第四节 一元复合函数 求导法则 本节内容: 一、多元复合函数求导的链式法则 二、多元复合函数的全微分 微分法则 机动 目录 上页 下页 返回 结束 多元复合函数的求导法则 第八章

一、多元复合函数求导的链式法则定理. 若函数u=(t),v=y(t)在点t可导,z=f(u,v)在点(u,v)处偏导连续，则复合函数 z= f(Φ(t), (t)在点t可导，且有链式法则dzOz du.Oz diOu dtay didt说明：若定理中f(u,v)在点(u,v)偏导数连续减弱为偏导数存在则定理结论不一定成立HIGHEDUCATIONPRESS机动目录下页返回结束上页

一、多元复合函数求导的链式法则 定理. 若函数 z = f (u,v) 处偏导连续, 在点 t 可导, t v v z t u u z t z d d d d d d     +   = z 则复合函数 且有链式法则 u v t t 机动 目录 上页 下页 返回 结束 说明: 若定理中 偏导数连续减弱为 偏导数存在, 则定理结论不一定成立

推广：设下面所涉及的函数都可微例如, z= f(u,v,w)1)中间变量多于两个的情形u=@(t),v=y(t), w=o(t)Oz dvzdwdzaz dudt ou dt 'Ov dt"owdt= fi''+ f'y'+ f'o"2）中间变量是多元函数的情形.例如z=f(u,v), u=p(x,y), v=y(x,y)Ozdz u0z Ov= figi+ f2yiOxduayddxzdzduX= fi'P2 + f2V2OvdyOudyHIGHEDUCATION PRESS机动目录下页返回结束上页

推广: 1) 中间变量多于两个的情形. 例如, z = f (u,v,w) , 设下面所涉及的函数都可微 . = t z d d = + +  1 2 3 f f f 2) 中间变量是多元函数的情形.例如, z = f (u,v) , u =  (x, y), v = (x, y) =   x z 11 21 = f   + f   1 2 2 2 = = f   + f     y z z z u v w u v x y x y t t t t u u z d d    t v v z d d    + t w w z d d    + x u u z      x v v z      + y u u z      y v v z      + 机动 目录 上页 下页 返回 结束 u =  (t), v = (t), w = (t)

又如, z=f(x,v), V=y(x,y)当它们都具有可微条件时，有atX= f' + f2 ViaxaxaxXdf070f2V2ayO2af不同，这里注意：oxxafOzox表示固定y对x求导表示固定对x求导ax口诀：分段用乘，分叉用加，单路全导，叉路偏导DLHIGHEDUCATIONPRESS机动目录上页下页返回结束

又如, z = f (x,v), v = (x, y) 当它们都具有可微条件时, 有 x z   1 21 = f  + f   y z   2 2 = f   z = f x x y 注意: 这里 x z   x f   x z   表示固定 y 对 x 求导, x f   表示固定 v 对 x 求导 口诀:分段用乘, 分叉用加, 单路全导, 叉路偏导 x f   = 与 不同, v 机动 目录 上页 下页 返回 结束

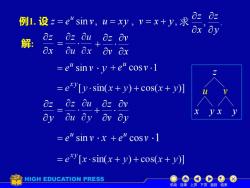
Oz0z例l.设z=e"sinv,u= xy，=x+y,求ax'Oyz auOz Ovdz解：axOu OxOv Oxsinv.y +eu cosv.l=eu= e*y[y· sin(x+ y)+ cos(x + y))dzOuOz OvVXyxQu ay+v ayaysinv.x +eu cosv.l=euO:y[x· sin(x + y)+ cos(x+ y)HIGH EDUCATION PRESS机动目录上页下页返回结束

例1. 设 z e sin v, u xy , v x y , u = = = + , . y z x z     求 解: x z   e v u = sin y z   e v u = sin x v v z      + e v u + cos y v v z      + e v u + cos 1 1 z u v x y x y 机动 目录 上页 下页 返回 结束

audu= x’sin y, 求例2. u= f(x,y,z)ox'oyaf azafdu解：axazxdx2xe2xsinysin+xt=2x(1+2xsinXaudafxy2Vsin2(y+xsin ycos yHIGH EDUCATION PRESS机动上页下页返回结束目录

例2. ( , , ) , sin , 2 2 2 2 u f x y z e z x y x y z = = = + + y u x u     求 , 解: x u   2 2 2 2 x y z xe + + = x y x y x x y e 2 2 4 2 2 2 sin 2 (1 2 sin ) + + = + x y z x y u y u   2 2 2 2 x y z ye + + = x y x y y x y y e 2 2 4 2 4 sin 2 ( sin cos ) + + = + x f   = 2 2 2 2 x y z ze + + + y f   = y z z f      + 2 2 2 2 x y z ze + + +  2 x sin y x cos y 2  机动 目录 上页 下页 返回 结束

dz例3.设 z=uv+sint,u=et,v=cost,求全导数dtdzdvdz oz du02解：dtOu dt?v dt?tvet-usint +cost=et(cost-sint)+costHIGHEDUCATION PRESS机动目录上页下页返回结束

例3. 设 z = uv + sin t , . d d t z z u v t t t t z d d t = v e e t t t t = (cos − sin ) + cos t u u z d d    = t z   + u = e t , v = cost , 求全导数 解: + cost 机动 目录 上页 下页 返回 结束

例4.设 w=f(x+y+z,xyz)，f具有二阶连续偏导数a?wow求w,f',f2Ox" 0x0z解：令u=x+y+z,v=xyz,则w= f(u, v)xyzxyzowx =Ji-1 + 2 y2= fi'(x+ y+z, xyz) +yz f2(x+ y+z, xyzW= fii-1+ fi2 ·xy +y f2+ yz[ f2i·1+ f22 ·xy]OxOz= fii + y(x + 2)fi2 + xyz f22 + y f2HIGH EDUCATION PRESS机动目录上页下页返回结束

为简便起见 , 引入记号 , , 2 1 12 u v f f u f f     =    = 例4. 设 f 具有二阶连续偏导数, 求 , . 2 x z w x w      解: 令 u = x + y + z , v = xyz, x w   w u v x y z x y z w = f (u, v) + f   yz 2 ( , ) 2 + y z f  x + y + z xyz 则 x z w    2 22 2 2 11 12 = f  + y(x + z) f  + xy z f  + y f  + f   xy 12 + f   x y 221 2 , f  , f  机动 目录 上页 下页 返回 结束

），求u的偏导数U=du-0--HIGH EDUCATION PRESS机动目录下页返回结束上页

=   x u 1 f  1 1 f y =  =   y u 1 f  2 + f  =   z u 2 f  2 1 2 1 f z f y x = − +  2 2 f z y = −  机动 目录 上页 下页 返回 结束 ，求u的偏导数

az= f(u,x,y), u=xey求axOxoy07f'ey + f2axa2=e'.fi+xe?y. fii+e'.fi3Oxoy+xe'.f21+ f23HIGH EDUCATION PRESS

=   x z 1 f  2 + f  =    x y z 2 11  f  13  f  21  f  23 + f  2 z x y    z x   求