《高等数学》课程教学资源（课件讲稿）第六章课件_6.6微分法在几何上的应用

微分法在几何上的应用一、空间曲线的切线和法平面定义 设 M是空间曲线L上的一个定点,M*是L上的一个动点，当M*沿曲线L趋于M时，割线MM*的极限位置MT（如果极限存在）称为曲线L在M处的切线。下面我们来导出空间曲线的切线方程

微分法在几何上的应用 一、空间曲线的切线和法平面 定义 设 M是空间曲线L 上的一个定点,M* 是 L 上的一个动点,当M* 沿曲线L 趋于M 时 , 割线MM*的极限位置 MT （如果极限存在）称为曲线L在M 处的切线。 下面我们来导出空间曲线的切线方程

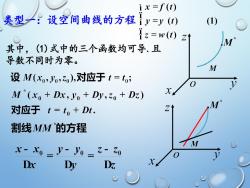
ix=f(t)类型一：设空间曲线的方程(1)iy=y (t)iz=w(t) ztM*其中，（1）式中的三个函数均可导.且导数不同时为零。M设 M(xo,Jo,zo),对应于 t = to;0LM*(xo + Dx, yo + Dy,zo + Dz)MZt对应于 t = to+ Dt.割线MM的方程MX- Xo-y- Jo- z- zoV0DxDz.Dy

类型一：设空间曲线的方程 其中，(1)式中的三个函数均可导.且 导数不同时为零

切线的过程考察割线趋近于极限位置上式分母同除以Dt.x- xo-y- o-z- zo当M*?M,即Dt?时DzDxDyDtDtDtX- Xo -J- yo - z- zo曲线在M处的切线方程fdto) y dto) wdto)切向量：切线的方向向量称为曲线的切向量T = (fdto)y d(to),wdto)法平面：过M点且与切线垂直的平面fto)(x- xo)+y to)(y- yo)+wdto)(z- zo)=0

考察割线趋近于极限位置——切线的过程 上式分母同除以 曲线在M处的切线方程 切向量：切线的方向向量称为曲线的切向量. 法平面：过M0点且与切线垂直的平面

例1求曲线口：解 当t=0时，x=0,=1,z=2,xe=e' cost, ye= 2cost - sint, ze=3e3tIxd0) =1, y(0) = 2, zd(0)=3,x-0y-1z-2切线方程23x+2(V-1)+3(z-2)=0法平面方程即x+2+3z-8=0

解 切线方程 法平面方程

iy=f(x)类型二：空间曲线方程i取x为参数iz=y (x)在M (xo, yo,zo)处,X- Xo-y- Jo- z- zo切线方程为fdx) y dx)1法平面方程为(x- x)+fdx)(y- yo)+y x)(z- zo)=0F(x,y,z)= 0类型三：空间曲线方程G(x,y,z) = 0六切向量-GGGG

类型二：空间曲线方程 取x为参数 法平面方程为 类型三：空间曲线方程 切向量

x-Xoy-Z- Z0yoFFFFF.F切线方程t77xG,GGGGGX7xl0V0法平面方程为FFFFF,F(7-z)=0XVoGGGGGCxoAV福例 2 求曲线x2□2z26解：将所给方程的两边对x求导并移项，得

切线方程 法平面方程为

dyz- xdzay+7-xdxdxdxV- zpdzdydz.x- y1dxdxidxy- zdz.dy=0,= - 1.dx (1,2.1)dx(1,- 2,1)T = (1, 0,- 1),由此得切向量x-1-y+27.所求切线方程为10法平面方程为（x-1)+0×+2)-（z-1)=0x- 7=(-

所求切线方程为 法平面方程为

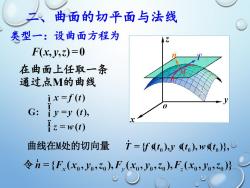
曲面的切平面与法线类型一：设曲面方程为7F(x, y,z)=0在曲面上任取一条通过点M的曲线ix=f(t)G: iy=y (t),1 z =w(t)T=(fdto),y dto),wdto)s,曲线在M处的切向量令={F(xo,Jo,zo),F,(x,yo,zo),F,(Xo,Jo,z))

二、曲面的切平面与法线 类型一：设曲面方程为 在曲面上任取一条 通过点M的曲线 曲线在M处的切向量 令

则nT，切平面方程为Fr(xo,Jo,zo)(x - Xo)+ F,(xo, o,zo)(y - yo)+ F,(xo, Jo,Zo)(z - zo) = 0通过点M（x，yo，z）而垂直于切平面的直线称为曲面在该点的法线X- XoZ- Z0y- yo法线方程为Fr(Xo,Yo,Z0)F(Xo, Yo,Zo)F,(Xo,yo,o)

则 切平面方程为 法线方程为

垂直于曲面上切平面的向量称为曲面的法向量曲面在M处的法向量即n ={Fi(Xo, Jo, z0),F,(Xo, Jo, zo),F,(Xo, Jo, z0))类型二：空间曲面方程形为 z= f（x，）令 F(x,y,z)=f(x,y)- z曲面在M处的切平面方程为f(xo,Jo)(x- xo)+ f,(xo,Jo)(y- yo)=z- zo曲面在M处的法线方程为x-Xo - y- yo7-70一f(xo,yo) f,(xo,Jo)

垂直于曲面上切平面的向量称为曲面的法向量. 曲面在M处的法向量即 类型二：空间曲面方程形为 令 曲面在M处的切平面方程为 曲面在M处的法线方程为