《高等数学》课程教学资源（PPT课件）第五章课件_第五章第一节课件

第五章，向量与空间解析几何第一节向量及其运算

第五章 向量与空间解析几何 第一节 向量及其运算

空间直角坐标系本章先引入空间直角坐标系，把点和有序数组、空间图形和代数方程联系起来，建立起对应关系，给数和代数方程以几何直观意义，从而可以利用代数方法研究空间图形的性质和相互关系；接着介绍向量概念，然后以向量代数为工具，重点讨论空间基本图类平面，直线，常用的曲面和曲线

一、空间直角坐标系 本章先引入空间直角坐标系，把点和有序数 组、空间图形和代数方程联系起来，建立起 对应关系，给数和代数方程以几何直观意义， 从而可以利用代数方法研究空间图形的性质 和相互关系；接着介绍向量概念，然后以向 量代数为工具，重点讨论空间基本图类—— 平面，直线，常用的曲面和曲线

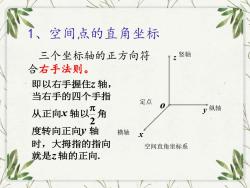
1、空间点的直角坐标竖轴三个坐标轴的正方向符合右手法则。即以右手握住z轴，当右手的四个手指定点从正向x轴以"角2度转向正向V轴横轴x时，大拇指的指向空间直角坐标系就是z轴的正向

横轴 x y 纵轴 z 竖轴 定点 o 空间直角坐标系 三个坐标轴的正方向符 合右手法则。 即以右手握住z 轴， 当右手的四个手指 从正向x 轴以 2 角 度转向正向y 轴 时，大拇指的指向 就是z轴的正向. 1、空间点的直角坐标

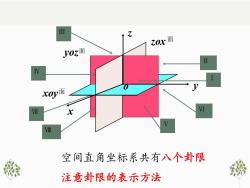
中zox面yoz面IIIV2xoy面VIVIxVIII空间直角坐标系共有八个卦限注意卦限的表示方法

Ⅶ x o y z xoy 面 yoz 面 zox 面 空间直角坐标系共有八个卦限 注意卦限的表示方法 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅷ

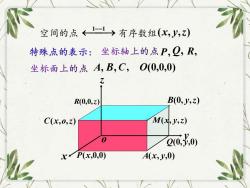
1空间的点 有序数组(x,y,z)特殊点的表示：坐标轴上的点P,Q,R坐标面上的点 A,B,C， O(0,0,0)ZB(0,y,z)R(0,0,z)M(x,y,z)C(x,0,z)@(0,y,0)0xP(x,0,0)A(x,y,0)

空间的点  ⎯→ 有序数组 (x, y,z) 1−−1 特殊点的表示: O(0,0,0) M(x, y,z) x y z o P(x,0,0) Q(0, y,0) R(0,0,z) A(x, y,0) B(0, y,z) C(x,o,z) P, Q, R, A, B, C

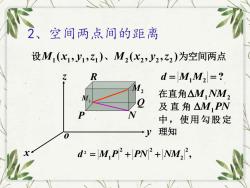
2、空间两点间的距离设M,(xi,J1,z)、M,(x2,2,z2)为空间两点Rd=MM =?7MF在直角△M,NMNQ及直角△M,PNPN中，使用勾股定 理知V0d? =[M,P +PN +[NM,[

设 ( , , ) 1 1 1 1 M x y z 、 ( , , ) 2 2 2 2 M x y z 为空间两点 x y z o M1 P N Q R M2 d = M1M2 = ? 在直角M1NM2 及直角 M1PN 中，使用勾股定 理知 , 2 2 2 2 1 d 2 = M P + PN + NM 2、空间两点间的距离

R[M,P =x2 -x[PM|= y2 - ylPN1[NM2 = [z2 - zl],. d = /M,P° +|PN} +[NM, lM,M2/ = /(x2 -x)+(y2 - y) +(z2 -z)空间两点间距离公式特殊地：若两点分别为M(x,y,z)，O(0,0,0)d =OM =/x+ y2+z?

,  M1P = x2 − x1 , 2 1 PN = y − y , 2 2 1 NM = z − z 2 2 2 2 d = M1P + PN + NM ( ) ( ) ( ) . 2 2 1 2 2 1 2 1 2 2 1 M M = x − x + y − y + z − z 空间两点间距离公式 特殊地：若两点分别为 M(x, y,z) , O(0,0,0) d = OM . 2 2 2 = x + y + z x y z o M1 P N Q R M2

例 1 求证以M,(4,3,1)、M,(7,1,2)、M,(5,2,3)三点为顶点的三角形是一个等腰三角形解 [M,M,2 = (7-4) +(1-3) +(2-1) =14,[M,M,° = (5 - 7) +(2 -1) +(3 - 2)° = 6,M,M,/ =(4 - 5) +(3 -2) +(1 - 3) = 6,:M,M=M,M，原结论成立

例 1 求证以 (4,3,1) M1 、 (7,1,2) M2 、 (5,2,3) M3 三点为顶点的三角形是一个等腰三角形. 解 = 2 M1M2 (7 4) (1 3) (2 1) 14, 2 2 2 − + − + − = = 2 M2M3 (5 7) (2 1) (3 2) 6, 2 2 2 − + − + − = = 2 M3M1 (4 5) (3 2) (1 3) 6, 2 2 2 − + − + − =  M2M3 , = M3M1 原结论成立

例2设P在x轴上，它到P(0,V2,3)的距离为到点P,(0,1,-1)的距离的两倍，求点P的坐标解因为P在x轴上,设P点坐标为(x,0,0),[PP|= /x2 +(/2) + 3° = /x2 +11,[PP|= /x2 +(-1) +1? = /x2 +2: PP|=2PPl, :. ~x2 +11=2~x2 +2→x=±1,，所求点为 (1,0,0),(-1,0,0)

例 2 设P在x轴上，它到 (0, 2,3) P1 的距离为 到点 (0,1, 1) P2 − 的距离的两倍，求点P的坐标. 解 因为P在x轴上， 设P点坐标为 (x,0,0), PP1 = ( ) 2 2 2 x + 2 + 3 11, 2 = x + PP2 = ( ) 2 2 2 x + − 1 + 1 2, 2 = x +  PP1 =2 , PP2 11 2  x + 2 2 2 = x +  x = 1, 所求点为 (1,0,0), (−1,0,0)

例. 在 z 轴上求与两点 A(-4,1,7)及B(3,5,-2)等距离的点：解：设该点为M(O,0,z),因为 MA=MB/(-4)? +12+(7 -z)2 = 3? +52+(-2 -z)2解得z=号，故所求点为M(0,0,号)思考：(1)如何求在xoy面上与A，B等距离之点的轨迹方程？2）如何求在空间与A，B等距离之点的轨迹方程

例. 在 z 轴上求与两点 A(−4,1,7) 解: 设该点为 M (0,0,z),因为 M A = MB , 2 (−4) 2 +1 2 + (7 − z) = 2 3 2 + 5 2 + (−2 − z) 解得 , 9 14 z = 故所求点为 及 B(3,5,− 2) (0,0, ). 9 M 14 思考: (1) 如何求在 xoy 面上与A , B 等距离之点的轨迹方程? (2) 如何求在空间与A , B 等距离之点的轨迹方程 ? 等距离的点