《高等数学》课程教学资源（PPT课件）第六章课件_6.1多元函数的概念、极限和连续

第一节元函数的概念、极限与连续一、区域二、多元函数的概念三、多元函数的极限四、多元函数的连续性HIGHEDUCATION PRESS目录下页返回结束机动上页

第一节 一、区域 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性 机动 目录 上页 下页 返回 结束 多元函数的概念、极限与连续

区域1.邻域点集U（Po.）=PPP<称为点P。的邻域例如,在平面上，U(Po,8 )=(x. )V(-x0)- +(1-10)- <8(圆邻域)在空间中，U(Po.8)= (x.1.=)/(x - x0)--(1- 30)-—(2-20)-(球邻域）说明：若不需要强调邻域半径，也可写成U(Po)0点P的去心邻域记为U（P）=PO<PP.<HIGHEDUCATIONPRESS机动目录上页下页返回结束

一、 区域 1. 邻域 点集 称为点 P0 的邻域. 例如,在平面上, (圆邻域) 在空间中, (球邻域) 说明：若不需要强调邻域半径 ,也可写成 点 P0 的去心邻域记为 机动 目录 上页 下页 返回 结束

因为方邻域与圆在讨论实际问题中也常使用方邻域，邻域可以互相包含0平面上的方邻域为U(Po.8 )= 3(x. 1)1X-x0<8.1-10<0HIGH EDUCATION PRESS机动目录上页下页返回结束

在讨论实际问题中也常使用方邻域, 平面上的方邻域为 。 因为方邻域与圆 邻域可以互相包含. 机动 目录 上页 下页 返回 结束

2. 区域外点、边界点(1) 内点、设有点集E及一点P：若存在点 P 的某邻域 U(P)c E则称P为E的内点；若存在点P的某邻域UPNE=@则称P为E的外点若对点 P的任一邻域U(P）既含E中的内点也含E的外点，则称P为E的边界点显然,E的内点必属于E，E的外点必不属于E，E的边界点可能属于E,也可能不属于EHIGH EDUCATION PRESS下页返回结束机动目录上页

2. 区域 (1) 内点、外点、边界点 设有点集 E 及一点 P : • 若存在点 P 的某邻域 U(P) E , • 若存在点 P 的某邻域 U(P)∩ E =  , • 若对点 P 的任一邻域 U(P) 既含 E中的内点也含 E 则称 P 为 E 的内点； 则称 P 为 E 的外点 ; 则称 P 为 E 的边界点 . 机动 目录 上页 下页 返回 结束 的外点 , 显然, E 的内点必属于 E , E 的外点必不属于 E , E 的 边界点可能属于 E, 也可能不属于 E

(2) 聚点若对任意给定的8，点P的去心邻域U(P.)内总有E中的点，则称P是E的聚点（因为聚点可以为聚点可以属于E，也可以不属于EE的边界点）所有聚点所成的点集成为E的导集HIGH EDUCATION PRESS目录上页下页返回结束机动

(2) 聚点 若对任意给定的 , 点P 的去心 机动 目录 上页 下页 返回 结束 邻域 内总有E 中的点 , 则 称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为 所有聚点所成的点集成为 E 的导集 . E 的边界点 )

开区域及闭区域(3)若点集E的点都是内点，则称E为开集福记作E：E的边界点的全体称为E的边界·若点集EE，则称E为闭集·若集D中任意两点都可用一完全属于D的折线相连则称D是连通的：D·连通的开集称为开区域简称区域；开区域连同它的边界一起称为闭区域HIGH EDUCATION PRESS目录下页返回机动上页结束

D (3) 开区域及闭区域 • 若点集 E 的点都是内点，则称 E 为开集； • 若点集 E E , 则称 E 为闭集； • 若集 D 中任意两点都可用一完全属于 D 的折线相连 , • 开区域连同它的边界一起称为闭区域. 则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; 机动 目录 上页 下页 返回 结束 。 。 • E 的边界点的全体称为 E 的边界, 记作E ;

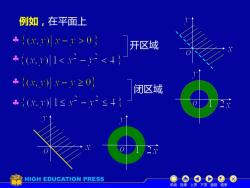
例如，在平面上*+(x.[1-1>0开区域<-*(1.1)(x.)|x-1≥0闭区域1≤*+(.)12.11HIGH EDUCATION PRESS目录上页下页返回结束机动

例如，在平面上 开区域 闭区域     机动 目录 上页 下页 返回 结束

整个平面是最大的开域也是最大的闭域；-1o点集（x)>是开集但非区域对区域D，若存在正数K，使一切点PeD与某定点A的距离「AP<K，则称D为有界域，否则称为无界域。HIGHEDUCATION PRESS机动目录上页下页返回结束

 整个平面  点集 是开集， 是最大的开域 , 也是最大的闭域； 但非区域 . 机动 目录 上页 下页 返回 结束 o • 对区域 D , 若存在正数 K , 使一切点 PD 与某定点 A 的距离 AP K , 则称 D 为有界域 , 界域 . 否则称为无

3. n维空间n元有序数组的全体称为n维空间(11.12.记作R".即R"=RxRx.xR=(i.2..x.x.R.k=1.2.....nn维空间中的每一个元素（"i."..",）称为空间中的一个点数称为该点的第k个坐标当所有坐标1=0时，称该元素为R"中的零元，记作HIGH EDUCATION PRESS目录下页返回结束机动上页

3. n 维空间 n 元有序数组 的全体称为 n 维空间, n 维空间中的每一个元素 称为空间中的 称为该点的第 k 个坐标 . 记作 即 机动 目录 上页 下页 返回 结束 一个点, 当所有坐标 称该元素为 中的零元,记作 O

R"中的点=(1.2...,)与点=(1.12..的距离记作p(.1）或x一，规定为p(. 1) =(11 - 11)- +(x- - 10+...-一1R"中的点=（1.."与零元○的距离为=+ +.+当n=1.2.3时.通常记作R"中的变元与定元a满足-→0记作→a.R"中点α的S邻域为U(a.8)=3xxER"p(x.a)<oHIGH EDUCATION PRESS机动目录上页下页返回结束

的距离记作 中点 a 的  邻域为 机动 目录 上页 下页 返回 结束 规定为 与零元 O 的距离为