《线性代数》课程教学课件（PPT讲稿，A）§6.2 基、坐标及其变换

线性代数 第六章s6.2基、坐标及其变换

线性代数 第六章 §6.2 基、坐标及其变换

线性代数 第六章一、线性空间的基与维数已知：在R中，线性无关的向量组最多由n个向量组成，而任意n+1个向量都是线性相关的问题：线性空间的一个重要特征在线性空间V中，最多能有多少线性无关的向量？

线性代数 第六章 一、线性空间的基与维数 已知：在 中，线性无关的向量组最多由 个向量组成，而任意 个向量都是线性相关的． R n n n + 1 问题：线性空间的一个重要特征——在线性空 间 V 中，最多能有多少线性无关的向量？

线性代数 第六章定义1在线性空间V中，如果存在n个元素α1,α2,.,αn,满足:(1)αi,α2,,α,线性无关(2）V中任一元素α总可由α,α2,,α,线性表示，那末，α,α2,…,α，就称为线性空间V的一个基，n称为线性空间V的维数

线性代数 第六章 (1) , , , ; 1 2  n线性无关 , . , , , , 1 2 基 称为线性空间 的维 数 那 末 就称为线性空间 的一个 n V     n V , (2) , , , 1 2 表 示 V中任一元素总可由    n线 性 定义１ 在线性空间 中，如果存在 n 个元素    n , , , 1 2  ,满足： V

线性代数 第六章维数为n的线性空间称为n维线性空间，记作V，当一个线性空间V中存在任意多个线性无关的向量时，就称V是无限维的，若α1,α2,,α,为V,的一个基,则V,可表示为Vn = (a = xja +xa, +...+x,anlxi,X2..,x, E R)

线性代数 第六章 , . 维数为n的线性空间称为n 维线性空间 记作Vn 若1 , 2 ,  , n为Vn的一个基,则Vn可表示为 Vn =  = x11 + x22 ++ xnn x1 , x2 ,  , xn  R 当一个线性空间 中存在任意多个线性无关 的向量时，就称 是无限维的． V V

线性代数 第六章元素在给定基下的坐标二、定义2设α,α,,α,是线性空间V,的一个基,对于任一元素αEV,总有且仅有一组有序数xi,X2,.",Xn,使α = Xai +x,α2 +...+Xnαn有序数组x,X2,,称为元素α在α,α2,,α这个基下的坐标,并记作 α=(xi,x2,,x,)

线性代数 第六章 ,  = x11 + x2 2 ++ xn n , ( , , , ) . , , , , , , 1 2 1 2 1 2 n T n n x x x x x x     =     基下的坐标 并记作 有序数组 称为元素 在 这 个 数 使 于任一元素 总有且仅有一组有序 设 是线性空间 的一个基 对 , , , , , , , , , 1 2 1 2 n n n n x x x V V     定义2    二、元素在给定基下的坐标

线性代数 第六章例1在线性空间P[xl,中,p,=1,p,=x,p,=x,px,p,=x就是它的一个基.例2次数不超过n的多项式的全体,记作P[xl,即P[x], =(p=a.x"+..+ax+aol an"ara.eR),对于通常的多项式加法，数乘多项式的乘法构成向量空间因此p在这个基下的坐标为(a0,a1,a2,a3,a4)

线性代数 第六章 2 4 1 2 3 4 3 4 5 [ ] , 1, , , , . P x x p p p p x x x p = = = = = 在线性空间 中 就是它的一个基 例1 p a x a x a x a1 x a0 2 2 3 3 4 4 4 = + + + + 任一不超过 次的多项式 p a p a p a p a p a p 0 1 1 2 2 3 3 4 4 5 = + + + + 可表示为 ( , , , , ) a0 a1 a2 a3 a4 p T 因此 在这个基下的坐标为 1 0 1 0 , , { , , , }, , . [ ] [ ] n n n n n n p x R P x P x = = + + +  a x a a a a a 次数不超过 的多项式的全体 记作 即 对于通常的多项式加法 数乘多项式的乘法构成向 量空间 例2

线性代数 第六章若取另—基1=1,2=1+X,3=2x2,4=x3s=x,则p=(ao-ai)qi+aq+a243+a344+a4q52因此p在这个基下的坐标为T(ao-a1,a1,=a2,a3,a4)注意：线性空间V的任一元素在不同的基下所对的坐标一般不同，一个元素在一个基下对应的坐标是唯一的

线性代数 第六章 注意: 则 若取另一基 , 1, 1 , 2 , , 4 5 3 4 2 1 2 3 q x q q x q x q x = = = + = = p a a q a q a q a q a q 0 1 1 1 2 2 3 3 4 4 5 2 1 = ( − ) + + + + , , ) 2 1 ( , , a0 a1 a1 a2 a3 a4 p T − 因此 在这个基下的坐标为 线性空间 的任一元素在不同的基下所对的 坐标一般不同，一个元素在一个基下对应的坐标是 唯一的． V

线性代数 第六章例2所有二阶实矩阵组成的集合对于矩阵的加法和数量乘法，构成实数域R上的一个线性空间．对于V中的矩阵0E12Ei=010E21E2200若kiE11+k2E12+k3E21+k4E22=0=ki=k2=k3=k3=0即E11,E12,E21,E22线性无关因此E11,E12,E21,E22为V的一组基

线性代数 第六章        =      =        =      = 0 1 0 0 , 1 0 0 0 , 0 0 0 1 , 0 0 1 0 21 22 11 12 E E E E 例2 所有二阶实矩阵组成的集合 ，对于矩阵 的加法和数量乘法，构成实数域 上的一个线性 空间．对于 中的矩阵 V V R , 0 0 0 0 1 1 1 2 1 2 3 2 1 4 2 2       k E + k E + k E + k E = O = 因此 若 0,  k1 = k2 = k3 = k3 = , , , . 即E1 1 E1 2 E2 1 E2 2线性无关 , , , . 因此 E1 1 E1 2 E2 1 E2 2为V的一组基

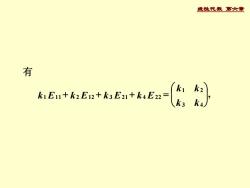
线性代数 第六章有k1k1E11+k2E12+k3E21+k4E22=k3k4

线性代数 第六章 , 3 4 1 2 1 1 1 2 1 2 3 2 1 4 2 2       + + + = k k k k k E k E k E k E 有

线性代数 第六章对于任意二阶实矩阵a11a12eV,A=a21a22)有A=a11E11+a12E12+a21E21+a22E22所以，矩阵A在这组基下的坐标是(a11, a12, a21, a22)

线性代数 第六章 A a1 1E1 1 a1 2E1 2 a2 1E2 1 a2 2E2 2 = + + + 有 , 2 1 2 2 1 1 1 2 V a a a a A       = 对于任意二阶实矩阵 ( , , , ) . a1 1 a1 2 a2 1 a2 2 A T 所以， 而矩阵 在这组基下的坐标是