《高等数学》课程教学资源（书籍教材）高等数学学习辅导——石油大学

高等数学学习辅导刘奋王玉凤陆晓光，主编中国石油大学数理系

高等数学学习辅导 刘奋 王玉凤 陆晓光 主编 中国石油大学数理系

前言高等数学是高等院校工科专业最重要的基础理论课之一，它不仅是学习后续课程以及在各个学科领域中进行理论研究和实践工作的必要基础，而且对学生能力的培养起着重要的作用。如何更好地指导学生学习这门课程，提高学习效率，解决疑难问题，加强自学辅导，加深对所学内容的理解和掌握，提高其综合运用知识解决实际问题的能力，我们编写了这本参考书。本书与教材《高等数学》（第五版，上、下册，高教出版社，同济大学编写）相配套，以国家教委颁发的高等学校工科《高等数学课程教学基本要求》为依据，总结了高等数学课程各章节的主要内容和基本要求；精选了各种类型的例题进行解题分析；配合教学内容，补充了较大信息量的练习题，并给出提示或解答。本书的许多内容，是长期执教高等数学的教师所积累的宝贵教学经验的总结，也是对教材内容的补充和扩展。这些内容，对于指导学生高等数学的学习，正确理解有关概念，澄清模糊认识，加强基本运算的训练，提高学习成绩培养创新能力和素质，都是很重要的。本书第一章由支丽霞编写，第二章由杨丽娜编写，第三章由穆铮编写，第四章、第五章由王玉凤编写，第六章、第十章由刘奋编写，第七章由李晓童编写，第八章、第九章由陆晓光编写，第十一章由陈安乐编写，第十二章由刘福江编写，在这里对他们的辛勤劳动表示诚挚的谢意。还要感谢数理系的领导、同仁对我们工作的大力支持和帮助，尤其是陈安乐老师、孙为老师和梁景伟老师。由于我们的水平有限，错误之处在所难免，请大家批评指正，编者2005年7月

前 言 高等数学是高等院校工科专业最重要的基础理论课之一，它不仅是学习后续课程以及 在各个学科领域中进行理论研究和实践工作的必要基础，而且对学生能力的培养起着重要的 作用。如何更好地指导学生学习这门课程，提高学习效率，解决疑难问题，加强自学辅导， 加深对所学内容的理解和掌握，提高其综合运用知识解决实际问题的能力， 我们编写了这 本参考书。 本书与教材《高等数学》（第五版，上、下册，高教出版社，同济大学编写）相配套， 以国家教委颁发的高等学校工科《高等数学课程教学基本要求》为依据，总结了高等数学课 程各章节的主要内容和基本要求；精选了各种类型的例题进行解题分析；配合教学内容，补 充了较大信息量的练习题，并给出提示或解答。本书的许多内容，是长期执教高等数学的教 师所积累的宝贵教学经验的总结，也是对教材内容的补充和扩展。这些内容，对于指导学生 高等数学的学习，正确理解有关概念，澄清模糊认识，加强基本运算的训练，提高学习成绩， 培养创新能力和素质，都是很重要的。 本书第一章由支丽霞编写，第二章由杨丽娜编写，第三章由穆铮编写，第四章、第五章 由王玉凤编写，第六章、第十章由刘奋编写，第七章由李晓童编写，第八章、第九章由陆晓 光编写，第十一章由陈安乐编写，第十二章由刘福江编写，在这里对他们的辛勤劳动表示诚 挚的谢意。 还要感谢数理系的领导、同仁对我们工作的大力支持和帮助，尤其是陈安乐老师、孙为 老师和梁景伟老师。 由于我们的水平有限，错误之处在所难免，请大家批评指正。 编 者 2005 年 7 月

目录第一章函数与极限(1)(26)第二章导数与微分·(37)第三章微分中值定理与导数的应用(72)第四章不定积分(90)第五章定积分第六章定积分·(108)第七章向量代数与空间解析几何(121)(132)第八章多元函数微分法及其应用(170)第九章重积分·第十章曲线积分与曲面积分(197)(221)第十一章无穷级数(238)第十二章微分方程

目 录 第一章 函数与极限.（1） 第二章 导数与微分.（26） 第三章 微分中值定理与导数的应用.（37） 第四章 不定积分.（72） 第五章 定积分.（90） 第六章 定积分.（108） 第七章 向量代数与空间解析几何.（121） 第八章 多元函数微分法及其应用.（132） 第九章 重积分.（170） 第十章 曲线积分与曲面积分.（197） 第十一章 无穷级数.（221） 第十二章 微分方程.（238）

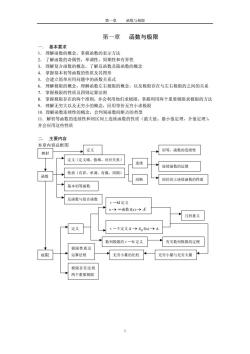
第一章函数与极限第一章函数与极限基本要求理解函数的概念，掌握函数的表示方法1.2.了解函数的奇偶性，单调性，周期性和有界性3.理解复合函数的概念，了解反函数及隐函数的概念4.掌握基本初等函数的性质及其图形5.会建立简单应用问题中的函数关系式理解极限的概念，理解函数左右极限的概念，以及极限存在与左右极限的之间的关系6.掌握极限的性质及四则运算法则7.8.掌握极限存在的两个准则，并会利用他们求极限，掌握利用两个重要极限求极限的方法理解无穷大以及无穷小的概念，回用等价无穷小求极限9.10.理解函数连续性的概念，会判别函数间断点的类型11.解初等函数的连续性和闭区间上连续函数的性质（最大值、最小值定理，介值定理），并会应用这些性质主要内容本章内容总框图定义初等、函数的连续性映射定义（定义域、值域、对应关系）连续连续函数的运算性质（有界、单调、奇偶、周期）函数间断闭区间上连续函数的性质基本初等函数反函数与复合函数一M定义x→函数 f(x)→A几何意义—8定义x→xf(x)→A定义数列极限的e—N定义有关数列极限的定理极限性质及极限运算法则无穷小量的比较无穷小量与无穷大量极限存在法则两个重要极限

第一章 函数与极限 第一章 函数与极限 一． 基本要求 1． 理解函数的概念，掌握函数的表示方法 2． 了解函数的奇偶性，单调性，周期性和有界性 3． 理解复合函数的概念，了解反函数及隐函数的概念 4． 掌握基本初等函数的性质及其图形 5． 会建立简单应用问题中的函数关系式 6． 理解极限的概念，理解函数左右极限的概念，以及极限存在与左右极限的之间的关系 7． 掌握极限的性质及四则运算法则 8． 掌握极限存在的两个准则，并会利用他们求极限，掌握利用两个重要极限求极限的方法 9． 理解无穷大以及无穷小的概念，回用等价无穷小求极限 10. 理解函数连续性的概念，会判别函数间断点的类型 11．解初等函数的连续性和闭区间上连续函数的性质（最大值、最小值定理，介值定理）， 并会应用这些性质 二． 主要内容 本章内容总框图 映射 定义 函数 反函数与复合函数 极限存在法则 两个重要极限 定义 极限性质及 运算法则 ε—M 定义 x→ ∞函数 f(x)→ A ε—δ定义 x → x0 f(x)→ A 数列极限的ε—N 定义 有关数列极限的定理 无穷小量与无穷大量 几何意义 极限 无穷小量的比较 定义（定义域、值域、对应关系） 连续 连续函数的运算 闭区间上连续函数的性质 初等、函数的连续性 间断 基本初等函数 性质（有界、单调、奇偶、周期） 1

第一章函数与极限1.函数1.函数的定义函数的分类有理整函数（多项式函数）有理函数代数函数有理分函数（分式函数）无理函数初等函数函数超越函数（非初等函数（分段函数）2.函数的性质(1）函数的有界性(2)函数的单调性(3）函数的奇偶性(4)函数的周期性3.反函数4.复合函数5.基本初等函数(1)幂函数=x"（u是常数)(a>0,a+1)(2)指数函数y=α(3）对数函数y=log。(a>0,a±1)(4)三角函数y=sinx,y=cosx,y=tanx,y=cotx(5)反三角函数y=arctanx,y=arccotx6.初等函数由常数和基本初等函数经过有限次四则运算和有限次的函数复合步骤所构成的并可用一个式子表示的函数7.双曲函数与反双曲函数e'-e"*双曲正弦shx-2e+e-r双曲余弦chx-2shxer-er双曲正切thx-chxe*+e-x2.极限1.极限的定义“—N"定义定义1Vs>0,3N>0,使n>N时，恒有x-a，记为limx,=a或x,→a（n-→8)2

第一章 函数与极限 1. 函数 1. 函数的定义 函数的分类 有理整函数（多项式函数） 有理函数 代数函数 有理分函数（分式函数） 无理函数 初等函数 函数 超越函数 非初等函数（分段函数） 2. 函数的性质 (1) 函数的有界性 (2) 函数的单调性 (3) 函数的奇偶性 (4) 函数的周期性 3. 反函数 4. 复合函数 5. 基本初等函数 (1) 幂函数 (μ是常数) µ y = x (2) 指数函数 y = a ( ) a > 0,a ≠1 x (3) 对数函数 y = log ( ) a > 0,a ≠1 x a (4) 三角函数 y = sin x, y = cos x, y = tan x, y = cot x (5) 反三角函数 y = arctan x, y = arccot x 6. 初等函数 由常数和基本初等函数经过有限次四则运算和有限次的函数复合步骤所构成的并可用一个 式子 表示的函数 7. 双曲函数与反双曲函数 双曲正弦 shx= 2 x x e e− − 双曲余弦 chx= 2 x x e e− + 双曲正切 thx= chx shx = x x x x e e e e − + − 2． 极限 1．极限的定义 “ε— N”定义 定义 1 ∀ε > 0 ,∃N > 0 ,使 n>N 时，恒有| xn − a |<ε ，记为 x a n n = →∞ lim 或 xn → a （ n → ∞） 2

第一章函数与极限“-”定义定义2>08>0，使当0x-x8时，恒有f(x)-A，记为lim=A或f(x)→A（当x→x）左极限V>0，>0，使当x-x时，恒有f(x)-A，记为limf(x)=A或f(x)=A,右极限>0，8>0，使当xx<x+时，恒有f(x)-A，记为limf(x)=A或f(x)=A定理：lim f(x)=Af(x)=f(x)=A2.无穷小与无穷大无穷小：极限为零的变量称为无穷小，记作limf(x)=0（或limf(x)=0）无穷大：绝对值无限增大的变量称为无穷大，记作limf(x)=80（或limf(x)=.co）无穷小与无穷大的关系在同一个极限过程中，无穷大的倒数为无穷小；恒不为零的无穷小的倒数为无穷大无穷小的运算性质定理1在同一极限过程中，有限个无穷小的代数和仍为无穷小定理2有界函数与无穷小的乘积是无穷小推论1在同一极限过程中，有极限的变量与无穷小的乘积是无穷小推论2常数与无穷小的乘积是无穷小推论3有限个无穷小的乘积也是无穷小3.极限的性质定理设limf(x)=A，limg(x)=B，则(1) lim[f(x)±g(x)= A±B(2) lim[f(x)·g(x)]= A·B(3 lim=，其中B0g(x)B推论1如果limf（x）存在，而c为常数，则lim[cf（x))=climf（x）推论2如果limf(x)存在，而n是正整数，则lim[f(x)}"=[limf(x)]"4．求极限的常用办法（1）用定义求之n

第一章 函数与极限 “ε −δ ”定义 定义 2 ∀ε > 0，∃δ > 0 ，使当0 0，∃δ > 0 ，使当 0 0 x −δ 0，∃δ > 0 ，使当 x0 < x < x0 +δ 时，恒有| f (x) − A |< ε ，记为 f x A x x = → + lim ( ) 0 或 f x = A + ( ) 0 定理： f x A f x f x A x x = ⇔ = = + − → lim ( ) ( ) ( ) 0 0 0 2．无穷小与无穷大 无穷小：极限为零的变量称为无穷小，记作 lim ( ) 0 0 = → f x x x （或lim ( ) = 0 →∞ f x x ） 无穷大：绝对值无限增大的变量称为无穷大，记作 = ∞ → lim ( ) 0 f x x x （或 = ∞ ） →∞ lim f (x) x 无穷小与无穷大的关系 在同一个极限过程中，无穷大的倒数为无穷小；恒不为零的无穷小的倒数为无穷大 无穷小的运算性质 定理 1 在同一极限过程中，有限个无穷小的代数和仍为无穷小 定理 2 有界函数与无穷小的乘积是无穷小 推论 1 在同一极限过程中，有极限的变量与无穷小的乘积是无穷小 推论 2 常数与无穷小的乘积是无穷小 推论 3 有限个无穷小的乘积也是无穷小 3．极限的性质 定理 设lim f (x) = A ，lim g(x) = B ，则 （1）lim[ f (x) ± g(x)] = A ± B （2）lim[ f (x)⋅ g(x)] = A⋅B （3） B A g x f x = ( ) ( ) lim ，其中 B ≠ 0 推论 1 如果lim f (x) 存在，而 c 为常数，则lim[cf (x)] = c lim f (x) 推论 2 如果lim f (x) 存在，而 n 是正整数，则 n n lim[ f (x)] = [lim f (x)] 4．求极限的常用办法 （1）用定义求之 3

第一章函数与极限（2）利用极限的四则运算法则（3）利用无穷小的运算性质求之（4）利用左右极限求分段函数极限（5）利用极限存在的两个准则求极限（6）利用两个重要极限求极限（7）利用等价无穷小代换求极限（7）利用初等函数的连续性求极限5.判定极限存在的准则准则I如果当xeU（xo，）（或|xM）时，有(2)lim,g(x)= A,lim(1) g(x)≤f(x)≤h(x)h(x)=A1-→0(-X-0)(x-00lim则（夹逼准则）f(x)存在，且等于Ar-→0(x→)准则Ⅱ单调有界数列必有极限6.两个重要极限sinx=1(2)lim(1+=)*=e或lim(1+x)*=e(1) lim-→0 x1-x7.无穷小的比较定义：设α，β是同一极限过程中的两个无穷小，且α≠0a%=0，就说β是比α高阶的无穷小，记作β=0(α)（1）如果lim-ββ（2）如果lim=C（C0），就说β与α是同阶的无穷小αβ特殊的如果lim=1，则称β与α是等阶的无穷小，记作α～βαβ（3）如果lim-C(C+0,K>O），就说β是α的K阶无穷小at8.等价无穷小的性质巴存在，则limB=limB'定理（等价无穷小替换定理）：设α～~α,β~β且limαaα"a9.极限的性质(1)唯一性(2）有界性（3）保号性（4）函数极限与数列极限的关系（与数列极限和其子列的极限的关系类似）10.连续1.连续的定义定义1若limAy=0或lim[f(x。+△x)-f(x。）=0则称函数y=f(x)在点x连续4

第一章 函数与极限 （2）利用极限的四则运算法则 （3）利用无穷小的运算性质求之 （4）利用左右极限求分段函数极限 （5）利用极限存在的两个准则求极限 （6）利用两个重要极限求极限 （7）利用等价无穷小代换求极限 （7）利用初等函数的连续性求极限 5．判定极限存在的准则 准则Ⅰ 如果当 x∈U 0 (x0 ,γ )（或| x |> M ）时，有 （1） g(x) ≤ f (x) ≤ h(x) （2） g x A x x x = → →∞ lim ( ) ( ) 0 ， h x A x x x = → →∞ lim ( ) ( ) 0 ) 则 lim ( )存在，且等于 A （夹逼准则） ( ) 0 0 f x x→x x→x 准则Ⅱ 单调有界数列必有极限 6．两个重要极限 （1） 1 sin lim 0 = → x x x （2） e x x x + = →∞ ) 1 lim(1 或 x e x x + = → 1 0 lim(1 ) 7．无穷小的比较 定义：设α ， β 是同一极限过程中的两个无穷小，且α ≠ 0 （1）如果lim = 0 β α ，就说 β 是比α 高阶的无穷小，记作 β = ο(α) （2）如果lim = C(C ≠ 0) α β ，就说 β 与α 是同阶的无穷小 特殊的如果lim =1 α β ，则称 β 与α 是等阶的无穷小，记作α ~ β （3）如果lim = C(C ≠ 0,K > 0) k α β ，就说 β 是α 的 K 阶无穷小 8．等价无穷小的性质 定理（等价无穷小替换定理）：设α ~ α',β ~ β '且 ' ' lim α β 存在，则 ' ' lim lim α β α β = 9．极限的性质 （1）唯一性 （2）有界性 （3）保号性 （4）函数极限与数列极限的关系（与数列极限和其子列的极限的关系类似） 10．连续 1.连续的定义 定义 1 若 lim 0 0 ∆ = ∆ → y x 或 lim[ ( ) ( )] 0 0 0 0 + ∆ − = ∆ → f x x f x x 则称函数 y = f (x) 在点 x0 连续 4

第一章函数与极限定义2若limf(x)=f(x。），则称函数y=f(x)在点x。连续定义3>0,3>0，当|x-x时，有f(x)-f(x)，则称函数=f(x)在点x连续1）单侧连续若函数f(x)在(a,x内有定义，且f(x）=f(x），则称f(x)在x。处左连续若函数f(x)在[xo,b)内有定义，且f(xt)=f(x。），则称f(x)在x。处右连续2）连续的充要条件定理f(x)在x处连续f(x)在x处既左连续又右连续3）间断点的定义函数f(x）在点x。处连续必须满足的三个条件：(1）f(x)在x。处有定义（2）limf(x)存在(3) lim f(x)=f(x)如果上述三个条件中只要一个不满足，则称函数f（x）在点x。处不连续（或间断），并称点x为f（x）的不连续点（或间断点）4）间断点的分类第一间断点[可去间断点((。)=(。)(。)。)存在)可跳跃间断点(()(）间断点第二间断点：无穷间断点，振荡间断点等(f(x。)f(x。至少有一个不存在)5）闭区间的连续性如果函数在开区间内（a,b）连续，并且在左端点x=a处右连续，在右端点x=b处左连续，则称函数f(x)在区间[a,b]上连续6)连续函数的运算性质f(x)定理1若函数f(x)，g(x)在点x处连续，则f(x)±g(x)，f(x)·g(x)，(g(x)±0)g(x)在点x。处也连续定理2严格单调的连续函数必有严格单调的反函数定理3若lim(x)=a，而函数f(x)在点a连续，则有limf[p(x))=f(a)=f(limp(x)5

第一章 函数与极限 定义 2 若 lim ( ) ( ) ，则称函数 0 o x x f x = f x → y = f (x) 在点 x0 连续 定义 3 ∀ε > 0,∃δ > 0 ，当| x − x0 |< δ 时，有| ( ) − ( )|< ε 0 f x f x ，则称函数 在点 连续 y = f (x) 0 x 1） 单侧连续 若函数 f (x) 在(a, x0 ]内有定义，且 f (x0 − ) = f (x0 ) ，则称 f (x) 在 x0 处左连续 若函数 f (x) 在[x0 ,b) 内有定义，且 f (x0 + ) = f (x0 ) ，则称 f (x) 在 x0 处右连续 2） 连续的充要条件 定理 f (x) 在 x0 处连续⇔ f (x) 在 x0 处既左连续又右连续 3） 间断点的定义 函数 f (x) 在点 x0 处连续必须满足的三个条件： （1） f (x) 在 x0 处有定义 （2） lim ( )存在 （3） 0 f x x→x lim ( ) ( ) 0 0 f x f x x x = → 如果上述三个条件中只要一个不满足，则称函数 在点 处不连续（或间断），并称点 为 的不连续点（或间断点） f (x) 0 x 0 x f (x) 4）间断点的分类 间断点 ( ) ( ) ( ) ( ) ( ) ( ) ⎪ ( ) ( ) ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ≠ = + − + − + − + − ( , ) : , ( ) ( ) ( , ) 0 0 0 0 0 0 0 0 至少有一个不存在 第二间断点 无穷间断点 振荡间断点等 跳跃间断点 可去间断点 存在 第一间断点 f x f x f x f x f x f x f x f x 5） 闭区间的连续性 如果函数在开区间内（a,b）连续，并且在左端点 x=a 处右连续，在右端点 x=b 处左连续，则称函 数 f (x) 在区间[a,b]上连续 6） 连续函数的运算性质 定理 1 若函数 f (x) ，g(x) 在点 x0 处连续，则 f (x) ± g(x) ，f (x)⋅ g(x) ， ( ) ( ) g x f x （ g(x0 ) ≠ 0 ） 在点 x0 处也连续 定理 2 严格单调的连续函数必有严格单调的反函数 定理 3 若 x a x x = → lim ( ) 0 ϕ ，而函数 f (x) 在点 a 连续，则有 lim [ ( )] ( ) (lim ( )) 0 0 f x f a f x x x x x ϕ ϕ → → = = 5

第一章函数与极限定理4设函数u=p(x)在点x=x连续，且p(x)=uo，而函数y=f(u)在点u=u连续，则复合函数y=f[p(x)在点x=x也连续7）初等函数的连续性定理1基本初等函数在定义域内是连续的定理2一切初等函数在其定义区间内都是连续的8）闭区间上连续函数的性质定理1（最大值最小值定理）在闭区间上连续的函数一定有最大值和最小值定理2（有界性定理）在闭区间上连续的函数一定在该区间上有界定理3（零点定理）设函数f(x）在闭区间[a,b]上连续，且f(a)与f(b)异号（即f(a)·f(b)0sgnx= 0x=0-1x<06

第一章 函数与极限 定理 4 设函数u = ϕ(x) 在点 x = x0 连续，且 0 0 ϕ(x ) = u ，而函数 y = f (u) 在点 连续，则 复合函数 u = u0 y = f [ϕ(x)] 在点 x = x0 也连续 7） 初等函数的连续性 定理 1 基本初等函数在定义域内是连续的 定理 2 一切初等函数在其定义区间内都是连续的 8） 闭区间上连续函数的性质 定理 1（最大值最小值定理） 在闭区间上连续的函数一定有最大值和最小值 定理 2（有界性定理） 在闭区间上连续的函数一定在该区间上有界 定理 3（零点定理）设函数 f (x) 在闭区间[a,b]上连续，且 f (a) 与 f (b) 异号（即 f (a)⋅ f (b) = 1 0 0 0 1 0 sgn x x x x 6

第一章函数与极限(2）y=f(x+a)+f(x-a)(a>0)的定义域[解题提示]：求复合函数的定义域，要注意内层函数的值域必须包含在外层函数的定义域内解：（1）易知当x≥0时，sgnx的值域包含在[0，1]，故y=f(sgnx)的定义域为[0,+o)(2）函数f(x+a)的定义域由不等式0≤x+a≤1解得-a≤x≤l-a，函数f(x-a)的定义域由不等式0≤x-a≤1解得a≤x≤a+111则a0)的定义域为[a,l-a];若0则1-aO)的定义域为为空集22类型三求复合函数和反函数x?[≤|≤1例3. 设f(x)=国>1’g(x)=lnx，求复合函数的解析式x2f(g(x)和g(f(x)[解题提示]：求复合函数一般采用代入法，即把一个函数的表达式代替另一个函数中的自变量解：先研究g(x)=lnx的值域与定义域的关系当x>e时，lnx>l：当01linxIn? xe-l e或01-2<x<1xx2例4. 求f(x)=1≤x≤2的反函数12<x≤4linx[解题提示]：求反函数的一般步骤为（1）把x从方程y=f（x)中解出；（2）把第一步所得表达式中的x与y对换，即得反函数解：求分段函数的反函数，只要分别求出个区间段的反函数及定义域即可7

第一章 函数与极限 （2） y = f (x + a) + f (x − a) (a > 0) 的定义域 [解题提示]：求复合函数的定义域，要注意内层函数的值域必须包含在外层函数的定义域内 解： （1）易知当 x ≥ 0时，sgn x 的值域包含在[0，1]，故 y = f (sgn x) 的定义域为[0,+∞) （2）函数 f (x + a) 的定义域由不等式0 ≤ x + a ≤ 1解得 − a ≤ x ≤ 1− a ，函数 的定义 域由不等式 解得 f (x − a) 0 ≤ x − a ≤ 1 a ≤ x ≤ a +1 若 2 1 0 0) 的定义域为[a,1− a]； 若 2 1 a > ，则 2 1 1− a 0) 的定义域为为空集 类型三 求复合函数和反函数 例 3．设 ( ) ⎪ ⎩ ⎪ ⎨ ⎧ > ≤ = 1 1 1 2 2 x x x x f x ， g(x) = ln x ，求复合函数的解析式 f (g(x)) 和 g( f (x)) [解题提示]：求复合函数一般采用代入法，即把一个函数的表达式代替另一个函数中的自变量 解： 先研究 g(x) = ln x 的值域与定义域的关系 当 x > e 时，ln x > 1；当 时， 1 0 − < ≤ = = ln ln 1 ln 0 ln 1 ( ( )) ln ( ) 2 2 x x x x g f x f x 例 4．求 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ < ≤ ≤ ≤ − < < = 2 4 ln 1 1 2 2 1 ( ) 2 2 x x x x x x f x 的反函数 [解题提示]：求反函数的一般步骤为（1）把 x 从方程 y = f (x)中解出；（2）把第一步所得表达式 中的 x 与 y 对换，即得反函数 解： 求分段函数的反函数，只要分别求出个区间段的反函数及定义域即可 7