《高等数学》课程教学资源（课件讲稿）第五章课件_第四次课

第五章第三节直线及其方程HIGH EDUCATION PRESS下页返回机动自录上贝结束

第三节 机动 目录 上页 下页 返回 结束 直线及其方程 第五章

一.一般式方程直线可视为两平面交线Ax+By+Ciz+D, = 0A2x+B2y+C2z+D2 = 0L说明:n1 = (A1,B1,Ci),n2 = (A2, B2, C2)Ⅱ对应不成比例HIGH EDUCATION PRESS下页返回机动目录上贝结束

x y z o 0 A1 x  B1 y  C1 z  D1  1 2 L 一. 一般式方程 直线可视为两平面交线 机动 目录 上页 下页 返回 结束 说明： 对应不成比例

二.对称式方程已知直线上一点M。(xo,yo,zo)和它的方向向量s=(m,n,p),求直线方程x-xoy-yoZ-ZOMo(xo,yo,-o)mpn说明：某些分母为零时，其分子也理解为零例如,当 m=n=0,p≠0 时，直线方程为x = Xoy= yoHIGH EDUCATION PRESS下页返回机动目录上贝结束

( , , ) 0 0 0 0 M x y z 二. 对称式方程 说明: 某些分母为零时, 其分子也理解为零. m x x  0      0 0 y y x x 求直线方程 n y y  0  p z z  0  直线方程为 s 已知直线上一点 ( , , ) 0 0 0 0 M x y z 例如, 当 m  n  0, p  0 时, 和它的方向向量 机动 目录 上页 下页 返回 结束

三.参数式方程x-xo y-yo2-设mnD得参数式方程X=xo+mty=yo +ntz=zo +ptHIGH EDUCATION PRESS下页返回机动录上贝结束

三. 参数式方程 设 得参数式方程 : t p z z n y y m x x       0 0 0 x  x  m t 0 y  y  n t 0 z  z  p t 0 机动 目录 上页 下页 返回 结束

例1.求过点(1,一2,4)且与平面2x-3y+z-4=0垂直的直线方程解：取已知平面的法向量n =(2, -3,1)为所求直线的方向向量n则直线的对称式方程为y+2x-1-HIGH EDUCATION PRESS返回机动目录上贝下页结束

解: 取已知平面的法向量 1 2  4    x  y z 则直线的对称式方程为 垂直的直线方程. 为所求直线的方向向量. 2  3 1 n  (2 ,  3, 1) n 例1. 求过点(1,－2 , 4) 且与平面 机动 目录 上页 下页 返回 结束

71-例2.求直线与平面22x+y+z-6=0的交点.解：所求直线的参数方程为x=2+ty=3+tz = 4+2t代入平面方程中，得解得t =-12(2+t)+(3+t)+(4+2t)-6= 0x =1, y= 2,z = 2所求交点坐标为HIGH EDUCATION PRESS

例2. 的交点. 求直线 与平面 解：所求直线的参数方程为 代入平面方程中，得 解得 所求交点坐标为

例3.用对称式及参数式表示直线x+y+z+l=02x-y+3z+4=0解：先在直线上找一点y+z=-2得y= 0, z=-2令x=1,解方程组y-3z=6 '故(1,0,-2)是直线上一点再求直线的方向向量Sni =(1,1,1),S = nj × n2n2 =(2, -1,3)HIGH EDUCATION PRESS下页返回机动目录上贝结束

例3.用对称式及参数式表示直线 解:先在直线上找一点. 3 6 2      y z y z 令 x = 1, 解方程组 ,得 y  0 , z  2 是直线上一点 . 机动 目录 上页 下页 返回 结束 再求直线的方向向量 s. 1 2  s  n  n

k= nxn2==(4,-1,-3)-1X一Z+故所给直线的对称式方程为x=1+4t参数式方程为y=-tz=-2-3tHIGHEDUCATION PRESS返回机动自录上贝下页结束

故所给直线的对称式方程为 参数式方程为  t 4 x 1 1  y  (4 ,  1,  3) 1 2 s  n  n 2 1 3 1 1 1   i j k 机动 目录 上页 下页 返回 结束

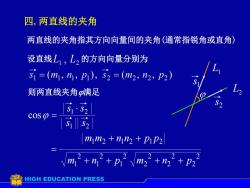
四.两直线的夹角两直线的夹角指其方向向量间的夹角（通常指锐角或直角）设直线L，，L，的方向向量分别为Si =(mi, ni, Pi), S2 =(m2, n2, P2)则两直线夹角?满足DScOS 3i ll 2mjm2 + njn2 + PiP2+nmtnmHIGHEDUCATIONPRESS

L2 L1  四. 两直线的夹角 则两直线夹角满足 1 2 设直线 L , L  两直线的夹角指其方向向量间的夹角(通常指锐角或直角) 的方向向量分别为 1 2 1 2 1 2 m m  n n  p p 2 1 2 1 2 1 m  n  p 2 2 2 2 2 2 m  n  p 1 2 1 2 cos s s s  s   1 s 2 s

>特殊情况：3i172(1) L L211mjm2 +njn2 + PiP2 = 0(2) Lj / L2si // 32mi- ni- Pim2n2P2例4求以下两直线的夹角x+y+2=0z+3x+2z=0HIGH EDUCATION PRESS

特殊情况: 1 2 (1) L  L 1 2 (2) L // L 0 m1 m2  n1 n2  p1 p2  2 1 2 1 2 1 p p n n m m   1 2 s  s 1 2 s // s 求以下两直线的夹角         2 0 2 0 : 2 x z x y L 例4