《线性代数》课程教学课件（PPT讲稿，A）5-3 相似矩阵

线性代数 第五章$ 5.3相似矩阵一、方阵的相似二、方阵可对角化的条件

线性代数 第五章 §5.3 相似矩阵 一、方阵的相似 二、方阵可对角化的条件

单选题0设置2分1、四阶方阵A的特征值为1、2、3、4，则air +a22 +a33 +a44IA|=8,1210,18P2410,9,24提交

线性代数 第五章 8, 12 10, 18 10, 24 9, 24 A B C D 提交 ， 1、四阶方阵A的特征值 为1、2、3、4 ，则 A = ； a a a a 11 + + + = 22 33 44 单选题 2分

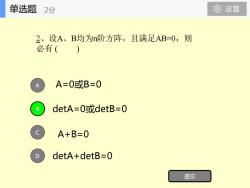
单选题0设置2分2、设A、B均为n阶方阵，且满足AB=0，则必有（)A=0或B=0detA=0或detB=0BA+B=0detA+detB=0提交

线性代数 第五章 A=0或B=0 detA=0或detB=0 detA+detB=0 A B C D 提交 2、设A、B均为n阶方阵，且满足AB=0，则 必有 ( ) A+B=0 单选题 2分

线性代数 第五章一、相似矩阵与相似变换的概念定义5.3.1设A.B都是n阶矩阵,若有可逆矩阵P.使P-IAP = B,则称B是A的相似矩阵,或说矩阵A与B相似.对A进行运算P-1AP称为对A进行相似变换，可逆矩阵P称为把A变成B的相似变换矩阵

线性代数 第五章 1 1 , , , , 5.3.1 , . , . A B n P P AP B B A A B A P AP A P A B − − = 设 都是 阶矩阵 若有可逆矩阵 使 则称 是 的 或说矩阵 与 相似 对 进 行运算 称为对 进行 可逆矩阵 称为把 变 相似 成 的 矩阵 相似变换 相 定 似变换矩阵 义 一、相似矩阵与相似变换的概念

线性代数第五章相似矩阵与相似变换的性质1.等价关系(1)自反性 A与本身相似;(2)对称性 A与B相似，则B与A相似;(3)传递性 A与B相似，B与C相似，则A与C相似2. P-I(AA,)P=(P-IA,P)(P-IA,P).3.若A与B相似,则Am与B相似(m为正整数）4.若n阶方阵A与B相似，则：(1) Tr(A)=Tr(B).(2) R(A)=R(B)(3) [A}=[Bl.（4）A与B等价

线性代数 第五章 1. 等价关系 1 1 1 1 2 1 2 2. ( ) ( )( ). P A A P P A P P A P − − − = 3.若A与B相似,则A 与B 相似(m为正整数). m m 相似矩阵与相似变换的性质 (1)自反性 A与本身相似； (2)对称性 A与B相似，则B与A相似； (3)传递性 A与B相似，B与C相似，则A与C相似. 4. 若n阶方阵A与B相似，则： （2）R(A)=R(B). （3）|A|=|B|. （4）A与B等价. （1）Tr(A)=Tr(B)

线性代数 第五章定理5.3.1若n阶矩阵A与B相似,则A与B的特征多项式相同,从而A与B的特征值亦相同证明：A与B相似=3可逆阵P,使得P-1AP=B:. B- aE|=P-IAP- P-1(aE)P=P-1(A-E)P=P-1[A- E|P=A-E

线性代数 第五章 证明： 1 A B P P AP B , 与 相似  = 可逆阵 使得 − B E P AP P (E)P −1 −1  − = − = P (A − E)P −1 = P A− E P −1 = A − E . 5.3.1 , , . n A B A B A B 若 阶矩阵 与 相似 则 与 的特征多项 式相同 从而 与 的特征值 定 亦相同 理

线性代数第五章推论1若阶方阵与对角阵[a元A=相似,则,22,,,即是A的n个特征值一般地，方阵A与对角阵相似，我们就称方阵A可对角化

线性代数 第五章 1 2 1 2 , , , , . 1 n n n A n            =         推 若 阶方阵与对角阵 相似 则 即是 的 个特征值 论 一般地，方阵A与对角阵相似，我们就称 方阵A可对角化

线性代数第五车二、方阵可对角化的条件定理5.3.2n阶方阵A可对角化的充要条件是A有n个线性无关的特征向量证明：假设存在可逆阵P,使P-IAP=Λ为对角阵把P用其列向量表示为P=[Pr,P2,…,Pn」[a由P-1AP= Λ,得AP = PA,2即 A[, 2 .]-[P, P2, .]=[aP1,2P2,.., ann]元

线性代数 第五章 证明: 1 P P AP , , − 假设存在可逆阵 使 = 为对角阵 1 2 , , , . P P p p p = n   把 用其列向量表示为   . 5.3.2 n A A n 阶方阵 可对角化的充要条件是 有 个线性无关的特 定 征向量 理 二、方阵可对角化的条件 1 2 1 2 1 2 , , , , , , n n n A p p p p p p              =          即 1 1 2 2 , , , . n n =      p p p   , , 1 =  =  − 由P AP 得AP P

线性代数 第五章". A[Pr, P2,..., Pn=[Ap1,Ap2,.., Apn=[aP,Pa,..a,Pn]于是有 Ap, = ^,P; (i=1,2,",n).可见入,是A的特征值,而P的列向量p，就是A的对应于特征值2.的特征向量又由于P可逆,所以pi,P2,…,P,线性无关反之，由于A恰好有n个线性无关的特征向量，这n个特征向量即可构成可逆矩阵P,使P-1AP=△

线性代数 第五章 1 2 1 2 1 1 2 2 , , , , , , , , , n n n n A p p p Ap Ap Ap    p p p  =         =     ( 1,2, , ). 于是有 Ap p i n i i i = =  , . i i i A P p A   可见 是 的特征值 而 的列向量 就是 的对应于特征值 的特征向量 1 2 , , , , . 又由于P p p p 可逆 所以 n 线性无关 1 , , , . A n n P P AP − =  反之 由于 恰好有 个线性无关的特征向量 这 个特征向量即可构成可逆矩阵 使

线性代数第五章说明如果A的特征方程有重根，此时不一定有n个线性无关的特征向量，从而矩阵A不一定能对角化，但如果能找到n个线性无关的特征向量A就能对角化，推论如果n阶矩阵A的n个特征值互不相等则A可对角化注意：矩阵A有n个不互不相等的特征值,只是A可对角化的充分条件，而非必要条件

线性代数 第五章 推论 如果n阶矩阵A的n个特征值互不相等， 则A可对角化． 说明 如果A的特征方程有重根，此时不一定有 n个线性无关的特征向量，从而矩阵A不一定能 对角化，但如果能找到n个线性无关的特征向量， A就能对角化． 注意：矩阵A有n个不互不相等的特征值,只是 A可对角化的充分条件，而非必要条件