《高等数学》课程教学资源（课件讲稿）7.4 一阶线性微分方程

第四节一阶线性微分方程一、线性方程二、 伯努利方程

第四节 一阶线性微分方程 一、线性方程 二、伯努利方程

第七章微分方程一、线性方程dy形如+P(x)y= Q(x)dx1.定义的方程，称为一阶线性微分方程若Q（x）三0,则称为齐次方程，若Q（x）丰0，则称为非齐次方程例如：y+ycosx=o为一阶齐次线性微分方程y'+ycosx =e-sinx为一阶非齐次线性微分方程第四节一阶线性微分方程

第四节 一阶线性微分方程 第七章 微分方程 1.定义 一、线性方程 例如: 形如

第七章微分方程2.解法dy步骤1解齐次方程+ P(x)y = 0dxdy分离变量-P(x)dxyP (x)dx + In|Cl两边积分得In/yl =y = Ce-J P(x)dx故通解为第四节一阶线性微分方程

第四节 一阶线性微分方程 第七章 微分方程 2. 解法 步骤1 解齐次方程 分离变量 两边积分得 故通解为

第七章微分方程dy+ P(x)y = Q(x)步骤2解非齐次方程dx用常数变易法：dy将齐次方程+ P(x)y = 0dx通解y= Ce-J P(x)dx中的C换成x的函数u(x).即做变换=u(x)e-P(x)dx从而待定出u(x)第四节一阶线性微分方程

第四节 一阶线性微分方程 第七章 微分方程 用常数变易法： 步骤2 解非齐次方程 从而待定出u(x)

设y= u(x)e-J P(x)dx, 于是dy= u'(x)e- J P(x)dx - u(x)P(x)e- P(x)dxdxdy代入非齐次方程+ P(x)y = Q(x),得dxu'(x)e-J P(x)dx - u(x)P(x)e-J P(x)dx + P(x)u(x)e-J P(x)dx = Q(x),u'(x) = Q(x)eJ P(x)dx即 u'(x)e-J P(x)dx = Q(x)

第四节 一阶线性微分方程 第七章 微分方程 于是

eJ P(x)dx dx + C.两边积分，得0(x)u:于是非齐次线性方程的通解为通解公式y= e-J P(x)dxQ(x)e P(x)dxdx + Cy = Ce-J P(x)dx + e-J P(x)dxp(x)dx dxQ(x)齐次方程通解非齐次方程特解

第四节 一阶线性微分方程 第七章 微分方程 于是非齐次线性方程的通解为 齐次方程通解 非齐次方程特解 通解公式

第七章微分方程3.典型例题dy2y5例1解方程1)2xdxx+1dy2dxdy2y解0,即先解dxx+ 1yx+ 1积分得Inlyl=2lnx+1I+ln|Cl，即y=C(×+1)2用常数变易法令y = u(x)· (x+ 1)2, 则 y = u · (x+ 1)2 + 2u· (x+ 1)23代入非齐次方程得u'=(x+1)2解得u=专(x+1)2+C故原方程通解为 =(x+ 1)2(x+1)2+c第四节一阶线性微分方程

第四节 一阶线性微分方程 第七章 微分方程 3. 典型例题 例1 解 即 积分得 即 用常数变易法. 则 代入非齐次方程得 解得 故原方程通解为 先解 令 y = C(x + 1) 2 y = u(x) ⋅ (x + 1) 2 , y ′ = u′ ⋅ (x + 1) 2 + 2u ⋅ (x + 1)

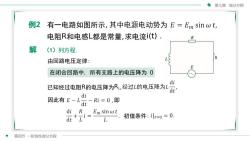
第七章微分方程例2有一电路如图所示，其中电源电动势为E=Emsinwt,电阻R和电感L都是常量,求电流i(t)，R解（1）列方程S由回路电压定律：E在闭合回路中，所有支路上的电压降为0di已知经过电阻R的电压降为R经过L的电压降为Ldt'di因此有E，Ri=0,即dtdiREm sin wt初值条件：ilt=0=01Ldt +第四节一阶线性微分方程

第四节 一阶线性微分方程 第七章 微分方程 在闭合回路中, 所有支路上的电压降为 0 解 （1）列方程. 因此有 即 初值条件: 由回路电压定律: 例2 有一电路如图所示, 电阻R和电感L都是常量,求电流i(t) . 已知经过电阻R的电压降为Ri

第七章微分方程Rdi.Em sin w tdt+iL即得到初值问题y=e-P(x)dxQ(x)e/ P(x)dxdx + Cilt=0= 0（2）解方程利用一阶线性方程解的公式可得En sin a te/atdt + qi(t) = e-JdtEmRR2 +w2)2(Rsin wt -wL cos wt)+ Ce-ttwLEm由初值条件：ilt=0=0得C=R2+ 2L2第四节一阶线性微分方程

第四节 一阶线性微分方程 第七章 微分方程 （2）解方程 由初值条件: 得 利用一阶线性方程解的公式可得 i(t) = + C 即得到初值问题

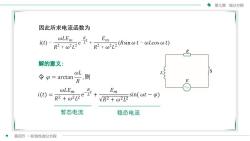
第七章微分方程因此所求电流函数为EmWLEmRi(t)1R? +a?r(Rsin w t - wLcos w t)R?+WL2R解的意义：SwL则令Φ=arctanREEmwLEmR.Ii(t)sin(wt-=eR2 + 2L2VR2+02L2暂态电流稳态电流第四节一阶线性微分方程

第四节 一阶线性微分方程 第七章 微分方程 暂态电流 稳态电流 因此所求电流函数为 解的意义: