《高等数学》课程教学资源（课件讲稿）1.7 无穷小的比较

第七节无穷小的比较一、无穷小的比较二、等价无穷小代换

一、无穷小的比较 二、等价无穷小代换 第七节 无穷小的比较

第一章函数与极限一、无穷小阶的比较在自变量统一变化过程中，两个无穷小之和、差、积仍为无穷小思考：两个无穷小之商是否还是无穷小？1t31-sin xxcos x=0Tlimlimlimlim -82x=0x2x2xx→0x-0 xx-→00.15反映出无穷小量趋于零的0.150.05快慢程度不一样！0.40.20.20.40.05/-0.11第七节无穷小的比较

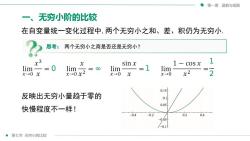
第七节 无穷小的比较 第一章 函数与极限 一、无穷小阶的比较 在自变量统一变化过程中,两个无穷小之和、差、积仍为无穷小. 反映出无穷小量趋于零的 快慢程度不一样！ 思考： 两个无穷小之商是否还是无穷小？ 0 ∞ 1 1 2

第一章函数与极限定义设α和β是同一自变量变化过程中的无穷小量且α≠0β（1）如果lim=0，则称β是比α高阶的无穷小，记作β=o(α);-αB（2）如果lim=80，则称β是比α低阶的无穷小αB（3）如果limC≠0，则称β与α是同阶无穷小二αβ特别地，如果lim==1，则称β与α是等价无穷小，记作α～βaβ（4）如果lim=C≠0,k>0,则称β是关于α的k阶无穷小qk第七节无穷小的比较

第七节 无穷小的比较 第一章 函数与极限 定义 设α和β是同一自变量变化过程中的无穷小量,且α ≠ 0. 则称β是比α 高阶的无穷小, 低阶的无穷小; 同阶无穷小; 则称β是比α 则称β与α是 则称β是关于α的 则称β与α是 记作 α~β. 记作 β=o(α);

第一章函数与极限例如：x3= 0,：×→0时,x3是x的高阶无穷小,即x3=0(x): limx→0 xx：x→0时,x是x2的低阶无穷小;: lim8,x=0 x2sinx：x→0时，sinx是x的等价无穷小，即sin日口1:limxx-011- cosx：x→0时,1一cosx是x2的同阶无穷小: lim2'x2x-→01一cosx是x的二阶无穷小11-cosx~L-121 - cos x是x?的等价无穷小，2第七节无穷小的比较

第七节 无穷小的比较 第一章 函数与极限 例如: 即 sinᵼ~ᵼ; 第七节 无穷小的比较 第一章 函数与极限

第一章函数与极限例1证明：当x→ 0时,"/1+x-1～=x.nN1+x-10证lim型an-bn=(a-b)(an-1+an-2b+...+abn-2+bn-1)Xx-00n("V1+x)"-1=limx~02("V1 + x)n-1 + ("1 +x)n=2 + . + 1n=lim1x=0 ("/1 + x)n-1 + ("V1+ x)++11：当x→0时，"1+x-1~=x.n第七节无穷小的比较

第七节 无穷小的比较 第一章 函数与极限 例1 证

第一章函数与极限β与α是等价无穷小的充分必要条件为β=α+o(α)定理1称α是β的主要部分ββ-α证必要性设日口limlim1=0αaα：β-α=o(α),即β=α+o(α)充分性设丰中中βα+o(α)o(α)lim= lim1lim+aααα日口.意义：用等价无穷小可给出函数的近似表达式，第七节无穷小的比较

第七节 无穷小的比较 第一章 函数与极限 定理1 β 与α 是等价无穷小的充分必要条件为β =α+o(α). 称α 是β 的主要部分. 证 必要性 充分性 设ᵼ~ᵼ, 设 ᵼ= ᵼ+ ᵼ(ᵼ)． ∴ ᵼ~ᵼ． = 1. 意义：用等价无穷小可给出函数的近似表达式． 第七节 无穷小的比较 第一章 函数与极限

第一章函数与极限例如：常用的等价无穷小及其它们的近似表达当凸时,当时,sinx~ x,sin x = x +o(x))tanx = x + o(x)tanx ~ x,arcsin x = x + o(x)arcsin x ～ x,11+21- cosx = **+ (),.1 - cos x ～2ex - 1 = x+o(x),ex-1~ x,In(1 + x) = x +o(x),In(1 +x) ~ x,n1+x-1=x+o(x)n1+x- 1 ~ x.第七节无穷小的比较

第七节 无穷小的比较 第一章 函数与极限 例如: 常用的等价无穷小及其它们的近似表达 当ᵼ→时ᵼ , 当ᵼ→ᵼ时, 第七节 无穷小的比较 第一章 函数与极限

第一章函数与极限等价无穷小代换定理2（等价无穷小代换定理）βBB设α～αβ～β,且lim二存在,则limlimαααIBBβαBαββ证limlimlimlim=limlim二Bαααααaα0定理2说明，对于型的极限选择恰当的等价无穷小可简化运算22xtan 2xlimlim例3：. x → 0时,sin(mx)~mx,tan(mx) ~mx.5x-=0 sin 5xx=0 5x第七节无穷小的比较

第七节 无穷小的比较 第一章 函数与极限 二、等价无穷小代换 定理2 (等价无穷小代换定理) 证 定理2说明, 对于   0 0 型的极限,选择恰当的等价无穷小可简化运算. 例3: 第七节 无穷小的比较 第一章 函数与极限

第一章函数与极限例5求极限7V1+x-1~-XV1+x2-1nlimcos x - 1x-01-COSE213(x2)21+ (x2)-= limlim31-cosxx-→0x-→02x2第七节无穷小的比较

第七节 无穷小的比较 第一章 函数与极限 例5 求极限 − 1 2 x 2 1 3 (x 2 ) 1 − cos ᵼ~ 1 2ᵼ2