《高等数学》课程教学资源（课件讲稿）3.7 曲率

曲率第七节一、弧微分曲率及其计算公式三、曲率圆与曲率半径*四、曲率中心的计算公式渐屈线与渐伸线

第七节 曲率 一、弧微分 三、曲率圆与曲率半径 二、曲率及其计算公式 *四、曲率中心的计算公式 渐屈线与渐伸线

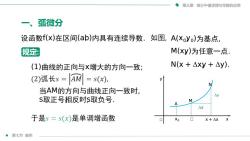
第三章微分中值定理与导数的应用一、弧微分设函数f(x)在区间(ab)内具有连续导数．如图，A(xoyo)为基点，M(xy)为任意一点，规定：N(x + △xy + y)(1)曲线的正向与x增大的方向一致；(2)弧长s =AM= s(x),y当AM的方向与曲线正向一致时Ays取正号相反时s取负号，MYAx于是s=s(x)是单调增函数口Xo0xX + △x第七节曲率

第七节 曲率 第三章 微分中值定理与导数的应用 一、弧微分 A x0 M ᵰ x + Δx x y ᵰ 规定: 设函数f(x)在区间(a,b)内具有连续导数. (1)曲线的正向与x增大的方向一致; 当AM的方向与曲线正向一致时, s取正号,相反时,s取负号. A(x0,y0)为基点, M(x,y)为任意一点. N(x + Δx,y + Δy). N Δx Δy

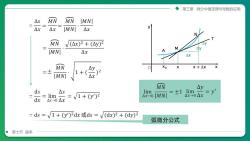
第三章微分中值定理与导数的应用MNMNAsIMN]yAx[MN]AxAxMN/(△x)? + (Ay)M1A[MN]AxAx+MNXoxX + △x口MNMNAydsAsJimlim±1AX-0MNAx-0Axlim1+(y)3dxAx-0△x:ds=/1+(y)2dx或ds=(dx)2+(dy)2弧微分公式第七节曲率

第七节 曲率 第三章 微分中值定理与导数的应用 弧微分公式 N T A x0 M x x + Δx x y ᵰ Δx Δy dy 第三章 微分中值定理与导数的应用 第七节 曲率

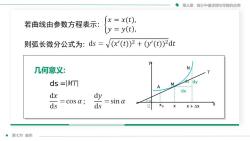
第三章微分中值定理与导数的应用(x = x(t),若曲线由参数方程表示：(y = y(t),则弧长微分公式为：ds=/(x'(t))2+(y'(t))2dtyN几何意义：idyds =|MTIMAdxdxdysina=cosα;?xdsdsXo口xX +△x第七节曲率

第七节 曲率 第三章 微分中值定理与导数的应用 则弧长微分公式为: 几何意义: 若曲线由参数方程表示: dx ds dy N T A x0 M x x + Δx x y ᵰ α ds =

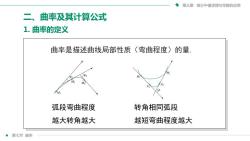
第三章微分中值定理与导数的应用曲率及其计算公式二E1.曲率的定义曲率是描述曲线局部性质（弯曲程度）的量MMM弧段弯曲程度转角相同弧段越大转角越大越短弯曲程度越大第七节曲率

第三章 微分中值定理与导数的应用 第七节 曲率 二、曲率及其计算公式 弧段弯曲程度 越大转角越大 转角相同弧段 越短弯曲程度越大 1. 曲率的定义

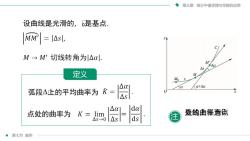
第三章微分中值定理与导数的应用设曲线是光滑的，是基点，MM |= [As],yiM→M'切线转角为|AαlMNOAs定义MMoAαKa+Aaa弧段A止的平均曲率为KxASdaAa梦线典体点点处的曲率为K= lim注ds△s△s-→0第七节曲率

第三章 微分中值定理与导数的应用 第七节 曲率 定义 直线上任意点 处的曲率为0. 注 设曲线ᵰ是光滑的, ᵰ0是基点. 弧段Δ上的平均曲率为 ᵰ 点ᵰ处的曲率为

第三章微分中值定理与导数的应用2.曲率的计算公式TT1(设: tanα = y'设手f（上阶可导）12: α = arctany'山曲率的dadx,112计算公式1+yyda又: ds =V1+y'2dx : Kds22第七节曲率

第七节 曲率 第三章 微分中值定理与导数的应用 2. 曲率的计算公式 曲率的 计算公式 设ᵰ= f()ᵰ二阶可导

第三章微分中值定理与导数的应用曲率公式说明：ly"|(1)当 ly'I<<1 时,有曲率近似计算公式K =3(1 + y'2)2(x = x(t),Ix'y" -x"y']给出，则K(2)若曲线由参数方程(y = y(t)(x'2 + y'2)2[x"|(3)若曲线方程为×=p(y),则K =(1 + x/2)2第七节曲率

第三章 微分中值定理与导数的应用 第七节 曲率 曲率公式说明: 有曲率近似计算公式 (3)若曲线方程为x = φ(y)

第三章微分中值定理与导数的应用例1计算等边双曲线日例2#抛物线+上在点(1,1)处的曲率哪一点的曲率最大？21解F 20：2解: yt3,[2al:K=3ly"[1 +(2ax + b)2]2.K:b(1 +y2)当x显然，时，K最大，x=1,y=12a即抛物线在顶点处的曲率最大V2232b2b-4ac[1 + (-1)2]22a4a第七节曲率

第七节 曲率 第三章 微分中值定理与导数的应用 例1 解 例2 解 计算等边双曲线ᵰᵰ= 1  在点(1,1)处的曲率. 抛物线 ᵰ= ᵰ 2 + ᵰᵰ+ ᵰ上 哪一点的曲率最大? ∵ ᵰ ′ = 2ᵰᵰ+ ᵰ, ᵰ ″ = 2ᵰ, 显然, 即抛物线在顶点处的曲率最大

第三章微分中值定理与导数的应用三、曲率圆与曲率半径设曲线主（在点处的曲率为（送0）在点处的曲线的法线上在凹的一侧取一点D1使IDMI一二=p一定义KJ以为圆心，为半径作圆（如图）D.称此圆为曲线在点M处的曲率圆（密切圆）My=f(x)曲率中心，曲率半径X第七节曲率

第三章 微分中值定理与导数的应用 第七节 曲率 定义 三、曲率圆与曲率半径 设曲线 ᵰ= ᵰ(ᵰ) 在点ᵰ(ᵰ,) 处的曲率为 ᵰ(ᵰ≠ 0). 以 ᵰ为圆心,  ᵰ为半径作圆(如图), 在点 ᵰ处的曲线的法线上,在凹的一侧取一点 D,  称此圆为曲线在点 M 处的曲率圆(密切圆). ᵰ         曲率中心, ᵰ         曲率半径