《高等数学》课程教学资源（课件讲稿）第一章_1.8函数的连续性与间断点

第节 函数的连续性与间断点函数的连续性二、 函数的间断点三、小结 思考题

第八节 函数的连续性与间断点 • 一、函数的连续性 • 二、函数的间断点 • 三、小结 思考题

函数的连续性1.函数的增量设变量u从它的一个初值u变到终值u,，终值与初值的差u，一u就叫做变量u的增量，记作Au即Au = u, -ur.注意：△u可以是正数也可以是负数

一、函数的连续性 1.函数的增量 1 2 2 1 2 1 . u u u u u u u u u u      设变量 从它的一个初值 变到终值 ，终值与 初值的差 就叫做变量 的增量，记作 ， 即 注意：u可以是正数也可以是负数

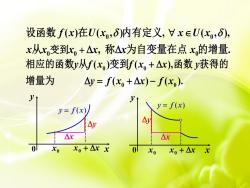
设函数 f(x)在U(xo,S)内有定义,V xeU(xo,),x从x变到x+△x，称Ax为自变量在点x,的增量相应的函数y从f(x,)变到f(x,+Ax),函数y获得的增量为Ay= f(x, +△r)- f(x)yyty=f(x)y=f(x))AyAyAxAr01xo+Ax xxo01xXo+AxXo

0 0 0 0 0 ( ) ( , ) , ( , ), , . f x U x x U x x x x x x x      变到   设函数 在 内有定义 从 称 为自变量在点 的增量 0 0 0 0 ( ) ( ), ( ) ( ). y f x f x x y y f x x f x        相应的函数 从 变到 函数 获得的 增量为 x y 0 0 x x  x 0 y  f ( x) x y x y 0 0 x x  x 0 x y y  f ( x)

2.连续的定义定义设函数y= f(x)在点x,的某个邻域内有定义，如果lim Ay = lim[f(x, + △x)- f(x,)] = 0Ax>0Ar-→0那么就称函数y=f(x)在点x,处连续设 x= x + △x,Ay= f(x)- f(x,),Ax→0 就是x→x,Ay→0就是 f(x)→f(x,)

2.连续的定义 , 0 设 x  x  x ( ) ( ), 0 y  f x  f x 0    x x x 0 , 就是 0 ( ) ( ). 0 y  就是 f x  f x 0 0 0 0 0 0 ( ) lim lim[ ( ) ( )] 0 ( ) . x x y f x x y f x x f x y f x x             设函数 在点 的某个邻域内有定义， 如果 那么就 定 称函数 在点 处连续 义

定义设函数y= f(x)在点x,的某个邻域内有定义，如果lim f(x) = f(x)x-→xo那么就称函数y=f(x)在点x,处连续"-S"定义:>0,>0,使当x-x<时,恒有|f(x)-f(x,)<8

"":    定义 0 0 0, 0, , ( ) ( ) . x x f x f x             使当 时 恒有 0 0 0 0 ( ) lim ( ) ( . ) ( ) x x y f x x f x f x y f x x     设函数 在点 的某个邻域内有定义， 如果 那么就 定义 称函数 在点 处连续

Ix+0,xsin在x= 0例1 试证函数f(x)=x0,x= 0,处连续。1证 lim x sin= = 0,x-→>0x又f(0)=0,lim f(x) = f(0),x-0由定义2知函数f(x)在x=0处连续

例1 . 0 0, 0, , 0, 1 sin ( ) 处连续 试证函数 在         x x x x x f x 证 0 1 lim sin 0, x x  x  又 f (0)  0, 由定义2知 函数 f (x)在 x  0处连续. lim ( ) (0), 0 f x f x  

3.单侧连续如果 lim f(x)=f(x)存在且等于f(x,)，即x-→xof(x) = f(x)就称函数f(x)在点x,左连续如果 lim f(x)=f(xt)存在且等于f(xo)，即x→xof(xt)= f(x,)就称函数f(x)在点x右连续定理函数f(x)在x,处连续台是函数f(x)在x酒处既左连续又右连续

3.单侧连续 0 0 ( ) ( ) . 函数 f x x f x x 在 处连续  是函数 在 处既左连续 定 又右连续 理 0 0 0 0 0 0 0 0 0 0 0 0 lim ( ) ( ) ( ) ( ) ( ) ( ) lim ( ) ( ) ( ) ( ) ( ) ( ) . x x x x f x f x f x f x f x f x x f x f x f x f x f x f x x             如果 存在且等于 ，即 就称函数 在点 ； 如果 存在且等于 ，即 就称函数 在点 左连续 右连续

x+2, x≥0.在x=0处的例2 讨论函数 f(x)=x-2, x<0,连续性。解 lim f(x) = lim(x +2) = 2= f(0)x-→0+x-→0+lim f(x) = lim(x -2)= -2± f(0),X-0x-0右连续但不左连续，故函数f(x)在点x=0处不连续

例2 . 0 2, 0, 2, 0, ( ) 连续性 讨论函数 在  处 的         x x x x x f x 解 lim ( ) lim( 2) 0 0       f x x x x  2 f (0), lim ( ) lim( 2) 0 0       f x x x x  2 f (0), 右连续但不左连续 , 故函数 f (x)在点x  0处不连续

4.连续函数与连续区间在区间上每一点都连续的函数，叫做在该区间上的连续函数,或者说函数在该区间上连续如果函数在开区间(a,b)内连续，并且在左端点x=a处右连续，在右端点x=b处左连续，则称函数f(x)在闭区间[a,bl上连续连续函数的图形是一条连续而不间断的曲线例如,有理函数在区间(一80,+8)内是连续的

4.连续函数与连续区间 在区间上每一点都连续的函数,叫做在该区间上 的连续函数,或者说函数在该区间上连续. ( ) [ , ] . , , ( , ) , 函 数 在闭区间 上连续 处右连续 在右端点 处左连续 则 称 如果函数在开区间 内连续 并且在左端点 f x a b x a x b a b   连续函数的图形是一条连续而不间断的曲线. 例如, 有理函数在区间( , )内是连续的

例3 证明函数 y= sinx在区间(-o0,+oo)内连续证任取x E (-0,+0),ArArAy = sin(x + △x)- sin x = 2sincos(x +22AxAr≤1, 则|Ay|≤ 2sincos(x+22对任意的α,当α0时，有sinα<α,Ar故Ay≤2sin<[Ax, : 当△x →0时,Ay → 0.2即函数y= sinx对任意xE(-o0,+oo)都是连续的

例 3 证 明函 数 y  sin x在区间( , )内连续. 证 任取 x (,), y  sin( x  x)  sin x ) 2 cos( 2 2sin x x x      cos( ) 1, 2x x    . 2 2sin x y  则   对任 意 的  , 0 , 当  时 有 sin ,   , 2 2sin x x y    故   当x  0时,y  0. 即函 数 y  sin x对任意 x ( , )都是连续的