《高等数学》课程教学资源（课件讲稿）第一章_1.6极限存在准则、两个重要极限

第六节极限存在准则两个重要极限极限存在准则二、两个重要极限三、小结 思考题

第六节 极限存在准则 两个重要极限 • 一、极限存在准则 • 二、两个重要极限 • 三、小结 思考题

一、夹逼准则准则I如果数列x,，J,及z，满足下列条件(n = 1,2,3...)(1) y, ≤x, ≤zn(2) lim yn = a,lim zn = a,n-n0那么数列x,的极限存在，且 limx,=a.n→证 :yn→a, zn→a,>0, N,>0,N,>0, 使得

一、夹逼准则 证 , , n n y a z a   1 2       0, 0, 0, N N 使得 , (1) ( 1,2,3 ) (2) lim , lim , li I m . n n n n n n n n n n n n n x y z y x z n y a z a x x a           如果数列 及 满足下列条件 那么数列 的极限存在，且 准则

当n>N时恒有y,-aN,时恒有z,-aN时, 恒有 a-<y,≤x,≤z<a+&,即x,-a<成立,.. lim x, = a.n-→8上述数列极限存在的准则可以推广到函数的极限

, 1 n  N y  a   当 时恒有 n max{ , }, 取 N  N1 N2 当 n  N时, 恒有 a    y  a  , 即 n , 2 n  N z  a   当 时恒有 n a    z  a  , n 上两式同时成立, a    y  x  z  a   , n n n 即 x  a   成立, n lim x a. n n    上述数列极限存在的准则可以推广到函数的极限

准则I' 如果当xεU(x,)(或|x>M)时，有(1) g(x)≤ f(x)≤h(x),(2) lim g(x) = A,lim h(x) = A,x→Xox→xo(x→00)(x-→0)那么 lim f(x)存在，且等于A.x-→xo(x→00)准则I和准则I‘称为夹逼准则注意：利用夹逼准则求极限关键是构造出y,与zn并且y,与z,的极限是容易求的

注意: 准则 Ⅰ和准则 Ⅰ′称为夹逼准则. 0 0 0 0 ( ) ( ) ( ) ( , )( ) (1) ( ) ( ) ( ), (2) lim ( ) , lim ( ) , lim ( ) . I o x x x x x x x x x x U x x M g x f x h x g x A h x A f x A                如果当 或| | 时，有 那么 存在，且等于 准则 , . n n n n y z y z 利用夹逼准则求极限关键是构造出 与 并且 与 的极限是容易求的

求 lim(例12n-+2+1+nVn'nM11nn解22+1Vn'+1+nVnVn+nvn1n又 limlim=21n-n-→>8n+n1十nnlimlim由夹逼定理得:12n-+1n→80n1+1lim() =1.22n-→Vn?+2+1+nVnVn

例1 2 2 2 1 1 1 lim( ). 1 2 n n n n n         求 解 2 2 2 2 1 1 , 1 1 n n n n n n n n         n n n n n n 1 1 1 lim 2 lim      又  1, 2 2 1 1 1 lim 1 lim n n n n n       1, 由夹逼定理得 2 2 2 1 1 1 lim( ) 1. 1 2 n n n n n         

练习设a>b>c>0,x,=a"+b"+c",求limxn>00a<x,<a.3解 由于以及lima./3= lima.3n =a.1lima = a,n→00n→n-0夹逼定理limx, = a.1n-→00练习:lim(2n)n-8福

解 由于 以及 lim , n a a   夹逼定理 lim . n n x a   a 1 lim 3 1 n n a a      3 n a  lim 3 n n a    0, , lim n n n n n n n a b c x a b c x   练习 设       求 n   x     2 2 2 1 1 1 lim 1 2 n n n n             练习：

证明lim/n =1练习n→8证：当n>1时n>l，记a,=n=1+h，则有n(n-1)n(n-1)h2h2 ≥n=(1+h,)"≥1+nh,+22220≤h或0≤h,≤<nn-1n-122于是1≤a,=1+h,≤1+而 lim1+1二n-1n→所以limn =1n0

lim 1 n n n   练习 证明  1 1 1 n n 证：当n n a n h      时, ，记 n n，则有 2 2 2 ( -1) ( -1) (1 ) 1 2 2 2 2 0 0 1 1 n n n n n n n n n n n n h nh h h h h n n             ， 或 2 2 1 1 1 lim1 1 1 1 lim 1 n n n n n a h n n n               于是 ，而 ， 所以

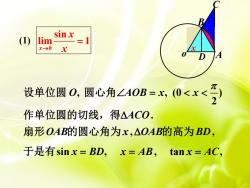
sinx(1)limx→0xX7AD元设单位圆 O,圆心角ZAOB= x,(0<x<一2作单位圆的切线，得△ACO.扇形OAB的圆心角为x,△OAB的高为BD，于是有sinx=BD， x=AB,tanx = AC

(1) 0 sin lim 1 x x  x  , , (0 ) 2 . , , sin , , tan , O AOB x x ACO OAB x OAB BD x BD x AB x AC           设单位圆 圆心角 作单位圆的切线，得 扇形 的圆心角为 的高为 于是有 A C x o B D

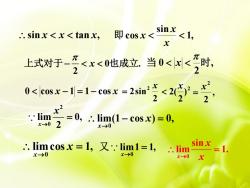
sinx即cosx<<1,.. sinx < x < tanx.x"时，元上式对于_元<x<0也成立。当0<x<22xx-20<|cosx-1 =1-cosx = 2sin22(?29lim= 0, :. lim(1 - cos x) = 0,2x-→0x-0sinx limcosx = 1, 又::lim1=1,=1...limx-→0x-0x-0X

sin x  x  tan x, 1, sin cos   x x 即 x 0 . 2 x  上式对于   也成立 , 2 当 0 时   x  0  cos x  1  1  cos x 2 2sin2 x  2 ) 2 2( x  , 2 2 x  2 0 lim 0, x 2 x   lim(1 cos ) 0, 0     x x limcos 1, 0    x x 0 lim1 1, x 又  0 sin lim 1. x x  x  

tanx例2. 求 limx-→0tanxsin x解： limlim-x-→0x-0xxcosx1sinx=1lim= limx-0x-0xcosxarcsin x例3. 求 limx-0x解：令t=arcsinx，则 x=sint，因此1t原式=limJimsintt-→0t-→0sintt

例2. 求 0 tan lim . x x  x 解: 0 0 tan sin 1 lim lim x x cos x x   x x x        0 0 sin 1 lim lim x x cos x   x x    1 例3. 求 0 arcsin lim . x x  x 解: 令 t x  arcsin , 则 x t  sin , 因此 原式 0 lim t sin t  t  0 1 lim t sin t t    1