《高等数学》课程教学资源（课件讲稿）第二章_2.5函数的微分

第五节西数的微分问题的提出、微分的概念三、 可微的条件四、微分在近似计算中的应用五、微分在估计误差中的应用六、小结

第五节 函数的微分 • 一、问题的提出 • 二、微分的概念 • 三、可微的条件 • 四、微分在近似计算中的应用 • 五、微分在估计误差中的应用 • 六、小结

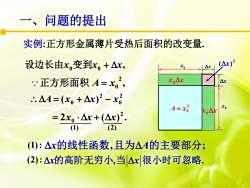
问题的提出实例：正方形金属薄片受热后面积的改变量(Ar)2设边长由x.变到x。+△x，AxLArAx：正方形面积A=x，.. A = (x, + Ax)2 - x)XoA=x:A= 2xo · Ax +(x)?(1)(2)(1)：△x的线性函数,且为△A的主要部分：(2)△x的高阶无穷小，当△x很小时可忽略

实例:正方形金属薄片受热后面积的改变量. 2 A = x0 x0 0 x , 0 0 设边长由x 变到x + x , 2 0 正方形面积 A = x 2 0 2 0 A = (x + x) − x 2 ( ) . 2 = x0  x + x (1) (2) x的线性函数,且为A的主要部分;   x x 的高阶无穷小, . 当 很小时可忽略 (1): (2): x x 2 (x) x x 0 x x 0 一、问题的提出

再例如,设函数y=x在点x.处的改变量为△x时，求函数的改变量△yAy =(x, + Ax)3 - x3= 3x .Ar +3x, ·(Ax) +(Ax)3(1)(2)当△x|很小时,(2)是△x的高阶无穷小o(△x),:. Ay ~ 3x? · Ax.既容易计算又是较好的近似值问题：这个线性函数(改变量的主要部分)是否所有函数的改变量都有？它是什么？如何求？

再例如, , . 0 3 x y y x x   = 为 时 求函数的改变量 设函数 在点 处的改变量 3 0 3 0 y = (x + x) − x 3 3 ( ) ( ) . 2 3 0 2 = x0  x + x  x + x (1) (2) 当 x 很小时, 3 . 2 y  x0  x (2)是x的高阶无穷小o(x), 既容易计算又是较好的近似值 问题:这个线性函数(改变量的主要部分)是否 所有函数的改变量都有?它是什么?如何求?

二、微分的概念设函数y= f(x)在某区间内有定义1.定义x,及x。+△x在这区间内，如果Ay = f(x, + Ax)- f(x) = A· △x +o(△x)成立(其中A是与△x无关的常数)，则称函数y=f(x)在点x,可微，并且称A·△x为函数y= f(x)在点x,相应于自变量增量△Ax的微分记作dy或df(x)，即dy=A·Ax.微分dy叫做函数增量△y的线性主部（微分的实质）

1.定义0 0 0 0 0 0 ( ) , , ( ) ( ) ( ) ( ), ( ) , ( ) , ( ), . y f x x x x y f x x f x A x o x A x y f x x A x y f x x x dy df x dy A x = +   = +  − =   +   =   =  =   设函数 在某区间内有定义 及 在这区间内 如果 成立 其中 是与 无关的常数 则称函数 在点 可微 并且称 为函数 在点 相应于自变量增量 的微分 记作 或 即 微分dy叫做函数增量 y的线性主部. (微分的实质) 二、微分的概念

由定义知：(1)dy是自变量的改变量△r的线性函数;(2)Ay-dy=o(△x)是比△x高阶无穷小;(3)当A±0时,dy与△Ay是等价无穷小：Ay0(△x)→1 (△x →0)dyA.△r（线性主部）；(4)当△x很小时,Ay~dy(5) A是与△x无关的常数,但与f(x)和x,有关

由定义知: ( ) ; 1 dy x 是自变量的改变量 的线性函数 ( ) ( ) ; 2  − =   y dy o x x 是比 高阶无穷小 ( ) , ; 3 0 当A dy y   时 与 是等价无穷小 dy y  A x o x   = + ( ) 1 → 1 (x → 0). 0 ( ) , ( ) . 5 A x f x x 是与 无关的常数 但与 和 有关 (4) , ( ); 当    x y dy 很小时 线性主部

2.可微的条件定理函数f(x)在点x,可微的充要条件是函数f(x)在点x,处可导,且 A= f'(x)证(1)必要性：f(x)在点x,可微o(△r)AyA-:. Ay = A . Ax + o(△xr)AxArAyo(△x)= A.则 limA+limArAr-→>0 AxAr-→0即函数f(x)在点x,可导，且A=f(x,)

0 0 0 ( ) ( ) , ( ). f x x f x x A f x =  函数 在点 可微的充要条件是函 数 在点 处可导 且 定理 证 (1) 必要性 ( ) ,  f x 在点x0可微 y = A x + o(x), , ( ) x o x A x y  = +   x o x A x y x x  = +  →   → ( ) lim lim 0 0 则 = A. ( ) , ( ). 0 0 即函数 f x 在点 x 可导 且A = f  x 2.可微的条件

(2)充分性：函数f(x)在点x可导Ay = f'(x),= f'(x0)+α,即limAr-→0 △xAr(△x → 0)从而 Ay = f'(x)·Ax+α·(Ax),: α→0= f'(x.). △x + o(△r),:函数f(x)在点x,可微，且f'(x)= A.：可导台可微A= f'(xo)函数y=f(x)在任意点x的微分，称为函数的微分，记作dy或df(x)，即dy=f(x)Ax

(2) 充分性 ( ) ( ), 从而 y = f  x0  x +  x ( ) , =  0 +   f x x y 即 ( ) , 函数f x 在点x0可导 lim ( ), 0 0 f x x y x =    →  → 0 (x → 0), ( ) ( ), 0 = f  x  x + o x ( ) , ( ) . 函数 f x 在点 x0可微 且 f  x0 = A . ( ). x0 可导  可微 A = f  ( ) , , ( ), ( ) . y f x x dy df x dy f x x = =   函数 在任意点 的微分 称为函数的 微分 记作 或 即

例1求函数y=x2当x=2，△x=0.02时的微分解 : dy= (x)Ax = 3xAx.= 0.24.= 3x△x.. dyx=2x=2Ax=0.02Ar=0.02通常把自变量x的增量△x称为自变量的微分记作dx，即dx =△x.dyf'(x).:. dy = f'(x)dx.dx即函数的微分dy与自变量的微分x之商等于该函数的导数.导数也叫微商

例 1 解 2, 0.02 . 求函数 y = x3 当 x x = 时的微分 dy = (x )x 3  3 . 2 = x x0.02 2 2 0.02 2 3  =  =  =  xx xx dy x x = 0.24. , , . x x dx dx x  =  通常把自变量 的增量 称为自变量的微分 记作 即 dy = f (x)dx. f (x). dx dy =  . " ". 即函数的微分dy dx 与自变量的微分 之商等于 该函数的导数 导数也叫 微商

y3.几何意义：(如图）N当△y是曲线的纵To(Ar)Aydy坐标增量时，dyMy= f(x)Ar就是切线纵坐标a对应的增量0Xo+AxxXo当△x很小时，在点M的附近，切线段MP可近似代替曲线段MN

y = f (x) 0x M N T dy yo(x) ） x yo  x 3.几何意义:(如图) . , 对应的增量 就是切线纵坐标 坐标增量时 当 是曲线的纵 dy y x + x 0 P , , . x M MP MN 当  很小时 在点 的附近 切线段 可近似代替曲线段

三、 微分的求法dy = f'(x)dx求法：计算函数的导数，乘以自变量的微分1.基本初等函数的微分公式d(x") = μuxu-'dxd(C) = 0d(sin x) = cos xdxd(cosx) = -sin xdxd(tan x) = sec xdxd(cot x) = -csc2 xdxd(secx) = sec x tan xdxd(cscx)=-cscxcotxdx

dy = f (x)dx 求法: 计算函数的导数, 乘以自变量的微分. 1.基本初等函数的微分公式 1 2 2 d( ) 0 d( ) d d(sin ) cos d d(cos ) sin d d(tan ) sec d d(cot ) csc d d(sec ) sec tan d d(csc ) csc cot d C x x x x x x x x x x x x x x x x x x x x x x x    − = = = = − = = − = = − 三、微分的求法