《高等数学》课程教学资源（课件讲稿）第六章_6.1定积分的元素法

第六章定积分的应用利用元素法解决：定积分在几何上的应用定积分在物理上的应用

第六章 利用元素法解决: 定积分在几何上的应用 定积分在物理上的应用 定积分的应用

第一节定积分的元素法问题的提出二、 小结-

第一节 定积分的元素法 • 一、问题的提出 • 二、小结

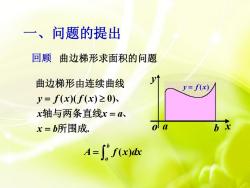
问题的提出一、回顾曲边梯形求面积的问题V曲边梯形由连续曲线y= f(x)y= f(x)(f(x)≥0)x轴与两条直线x=ab xolax=b所围成。A= J' f(x)dx

回顾 曲边梯形求面积的问题 一、问题的提出 a b x y o y  f (x) ( )( ( ) 0) . y f x f x x x a x b     曲边梯形由连续曲线 、 轴与两条直线 、 所围成 ( ) b a A f x dx  

面积表示为定积分的步骤如下(1)把区间[a,b]分成n个长度为4x,的小区间相应的曲边梯形被分成n个窄曲边梯形，第个窄曲边梯形的面积为△A，则A=4A,i-1(2）计算△A,的近似值AA, ~ f(5)4x;S; E Ax,A~Zf(5,)x.(3)求和，得A的近似值i=1

面积表示为定积分的步骤如下 ( )      A f x x i i i i i   (3) 求和，得A的近似值 ( ) . 1 i i n i A   f x   (2) Ai 计算 的近似值 1 (1) [ , ] i n i i i a b n x n i A A A       把区间 分成 个长度为 的小区间， 相应的曲边梯形被分成 个窄曲边梯形，第 个 窄曲边梯形的面积为 ，则

(4)求极限，得A的精确值面积元素nZ f(5)Ax; = [" f(x)dxA = lim1-→0i1关键：若用△A表示任一小区间dA[x,x+dx]上的窄曲边梯形的面积则A=Z4A, 并取△A~f(x)dx,f(x)V手Ef(x)dx于是A～记 dA=f(x)dx，称为面积元素，a xx+dkbx则A= lim Ef(x)dx = f'f(x)dx

(4) 求极限，得A的精确值 i i n i A   f x   lim ( ) 1 0     b a f (x)dx 则A f x dx  lim ( )  ( ) .   b a f x dx 记 d ( ) A f x dx  ，称为面积元素， y  f (x) a b x y o dA 面 积 元 素 x x  dx [ , ] ( ) ( ) A x x dx A A A f x dx A f x dx          若用 表示任一小区间 上的窄曲边梯形的面积， 则 ，并取 ， 于是 关键：

一般的，当所求量U符合下列条件：(1)U是与一个变量x的变化区间[a,b]有关的量;(2)U对于区间[a,b具有可加性，就是说，如果把区间[a,b分成许多个部分区间，则U的相应地分成许多部分量，而U等于所有部分量之和；(3)部分量△U,的近似值可表示为f(5)△x;;就可以考虑用定积分来表达这个量U--元素法

一般的，当所求量U符合下列条件： (1) U是与一个变量x的变化区间[a,b]有关的量； (2) U对于区间[a,b]具有可加性，就是说，如果 把区间[a,b]分成许多个部分区间，则U的相应地 分成许多部分量，而U等于所有部分量之和； (3) ( ) ; U f x i i i 部分量  的近似值可表示为  就可以考虑用定积分来表达这个量U. -元素法

元素法的一般步骤：1）根据问题的具体情况，选取一个变量例如X为积分变量，并确定它的变化区间[a,b];2)设想把区间[a,b]分成n个小区间，取其中任一小区间并记作[x,x+dx]，求出相应于这小区间的部分量AU的近似值.如果△U能近似地表示为[a,bl上的一个连续函数在x处的值f(x)与dx的乘积，就把f(x)dx称为量U的元素，且记作dU,即dU=f(x)dx;

元素法的一般步骤： 1）根据问题的具体情况，选取一个变量例如 x 为积分变量，并确定它的变化区间[a,b]； 2) [ , ] [ , ] . [ , ] ( ) ( ) ( ) a b n x x dx U U a b x f x dx f x dx U dU dU f x dx     设想把区间 分成 个小区间，取其中任 一小区间并记作 ，求出相应于这小区 间的部分量 的近似值 如果 能近似地表示 为 上的一个连续函数在 处的值 与 的乘积，就把 称为量 的元素，且记作 ，即 ；

3）以所求量U的元素f(x)dx为被积表达式，在区间[a,b]上作定积分，得U={~f(x)dx,即为所求量U的积分表达式这个方法通常叫做元素法应用方向：平面图形的面积；：体积；平面曲线的弧长；功；水压力；引力等

这个方法通常叫做元素法． 应用方向： 平面图形的面积；体积；平面曲线的弧长； 功；水压力；引力等． 3) ( ) [ , ] ( ) . b a U f x dx a b U f x dx U   以所求量 的元素 为被积表达式，在 区间 上作定积分，得 ， 即为所求量 的积分表达式

二、小结元素法的提出、思想、步骤（注意微元法的本质）

元素法的提出、思想、步骤. （注意微元法的本质） 二、小结