《高等数学》课程教学资源（课件讲稿）第五章_5.4反常积分

第四节反常积分一、无穷限的反常积分二、无界函数的反常积分·三、小结

第四节 反常积分 • 一、无穷限的反常积分 • 二、无界函数的反常积分 • 三、小结

无穷限的反常积分定义1 设函数f(x)在区间[a,+)上连续，取b>a如果极限 lim「"f(x)dx存在，则称此极限为函数f(x)在区间[a,+o0)上的反常积分，记作[f(x)dx" f(x)dx = lim [" f(x)dx当极限存在时，称反常积分收敛：当极限不存在时，称反常积分发散

一、无穷限的反常积分 1 ( ) [ , ) lim ( ) ( ) [ , ) ( ) ( ) lim ( ) . b b a a b a a b f x a b a f x dx f x a f x dx f x dx f x dx →+ + + →+ +  + =     定义 设函数 在区间 上连续，取 如果极限 存在，则称此极限为函数 在区间 上的 记作 当极 反常积分， 限存在时，称反常积分收敛；当极限不存在 时，称反常积分发散

类似的，设函数f(x)在区间(-80,b上连续，取a<b如果极限lim「"(x)dx存在，则称此极限为函数f(x)在区间(-o,b)上的反常积分，记作[ f(x)dx", f(x)dx= lim f' f(x)dx当极限存在时，称反常积分收敛：当极限不存在时，称反常积分发散

( ) ( , ] lim ( ) ( ) ( , ] ( ) ( ) lim ( ) . b a a b b b a a f x b a b f x dx f x b f x dx f x dx f x dx →− − − →− −   −  =     类似的，设函数 在区间 上连续，取 如果极限 存在，则称此极限为函 数 在区间 上的反常积分，记 反常积分收敛 作 当极限存在时，称 ；当极限不 反常积 存 时，称 分发散 在

设函数f(x)在区间(-0,+)上连续，如果反常积分[~ f(x)dx和J f(x)dx都收敛，则称上述两反常积分之和为函数f(x)在无穷区间(-80,+80)上的反常积分，记作:J f(x)dx- f(x)dx = J (x)dx+ Jt° f(x)dx= lim (" f(x)dx+ lim [' f(x)dxh+oa极限存在则称反常积分收敛：否则，称反常积分发散

0 0 0 0 ( ) ( ) ( ) lim ( ) lim ( ) b a b a f x dx f x dx f x dx f x dx f x dx + + − − →− →+ = + = +      0 0 ( ) ( , ) ( ) ( ) ( ) ( , ) ( ) f x f x dx f x dx f x f x dx + − + − − + − +    设函数 在区间 上连续，如果反常 积分 和 都收敛 反常积分， ，则称上述 两反常积分之和为函数 在无穷区间 上的 记作： 极限存在则称反常积分收敛；否则，称反常积分发散

几何意义若反常积分f(x)dx收敛,且f(x)≥ 0 ,x E [a,+o0),则其几何意义是：曲线y=f(x)，x=a,x轴所围的开口曲边三角形的面积存在，且为ft* f(x)dx.y=f (网)这时x轴是曲线y=f(α)的水平渐近线Oa

几何意义 若反常积分  + a f (x)dx 收敛， 则其几何意义是： 曲边三角形的面积存在，且为 ( )d .  + a f x x 这时 x 轴是曲线y = f (x)的水平 渐近线. 且f (x)  0 , x  [a , +), 曲线 y = f (x) , x = a , x 轴所围的开口 a x y y = f (x) O

若反常积分[f(x)dx 收敛, 且f (x)≥0 ,x E (-o0 , bl,则其几何意义是：曲线y=f(x)，x=b，x轴所围的开口曲边三角形的面积存在，且为f(x)dx.这时x轴是曲线y=f(x）的水平渐近线y=f()xOb

若反常积分 − b f (x)dx 收敛， 则其几何意义是： 曲边三角形的面积存在，且为 ( )d . − b f x x 曲线y = f (x)的水平渐近线. 且f (x)  0 , x  (- , b], 曲线 y = f (x) , x = b , x 轴所围的开口 b x y y = f (x) O 这时 x 轴是

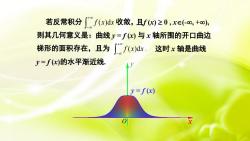
若反常积分[f (x)dx 收敛, 且f(x) ≥ 0 ,xe(-00, +o0),则其几何意义是：曲线=f(x)与x轴所围的开口曲边梯形的面积存在，且为f(x)dx.这时x轴是曲线y=f(x)的水平渐近线y=f(x)O

若反常积分  + − f (x)dx 收敛， 则其几何意义是： 梯形的面积存在，且为 ( )d .  + − f x x y = f (x)的水平渐近线. 且f (x)  0 , x(-, +), 曲线 y = f (x) 与 x 轴所围的开口曲边 x y y = f (x) O 这时 x 轴是曲线

dx*+00例1计算反常积分1+x20dxdxdxco+8+00解十1+x2Jo1+-00yYOV=limdx + limdx1+x222b-→+Jo1 +xJa1+xa→-00= lim [arctan x], + lim [arctan x]§0-8b=(-)+=-lim arctana + lim arctanb=元.b-→+00a→-00

例1 计算反常积分 . 1  2 + − + x dx 解  + − + 2 1 x dx − + = 0 2 1 x dx  + + + 0 2 1 x dx  + = →− 0 2 1 1 lim a a dx x  + + →+ b b dx x 0 2 1 1 lim   0 lim arctan a a x →− =  0 lim arctan b b x →+ + a a lim arctan →− = − b b lim arctan →+ + . 2 2 =    +       = − x o y 2 1 1 y x = +

若F(αx)是f(x)的原函数引入记号F(+o0)= lim F(x); F(-0)= lim F(x)X→-00→+8则有类似牛一莱公式的计算表达式：+8= F(+oo)-F(a)[+° f(x)dx = F(x)b[ f(x)dx= F(x)= F(b)- F(-80)-8+8[~ (x)dx = F(x)= F(+)-F(-8)-8

若F x f x ( ) ( ) , 是 的原函数 引入记号 ( ) lim ( ) ; x F F x → + + = ( ) lim ( ) x F F x → − − = 则有类似牛 – 莱公式的计算表达式 : ( )d a f x x +   = F x( ) a + = + − F F a ( ) ( ) ( )d b f x x  −  b − = − − F b F ( ) ( ) f x x ( )d +   −  + − = + − − F F ( ) ( ) = F x( ) = F x( )

例2证明反常积分dx当p>1时收敛，4当p≤1时发散.（第一类p积分）证 (1) p= 1,** dx= _dx =[In x]°= +,[+80, p1时反常积分收敛，其值为p-ii当p≤1时反常积分发散

证 (1) p = 1, + 1 1 dx x p  + = 1 1 dx x   + = 1 ln x = +, (2) p  1,  + 1 1 dx x p + −       − = 1 1 1 p x p      − +   = , 1 1 1 , 1 p p p 因此当 p  1时反常积分收敛，其值为 1 1 p − ； 当 p  1时反常积分发散. 1 1 2 1 1 ( ) p dx p x p p +   例 证明反常积分 当 时收敛， 当 时发散.第一类 积分