《高等数学》课程教学资源（课件讲稿）第四章_4.3分部积分

第三节分部积分基本内容二、 例题三、 小结四、 思考题

第三节 分部积分 • 一、基本内容 • 二、例题 • 三、小结 • 四、思考题

一、基本内容设函数u=u(x)和v=v(x)具有连续导数(uv) = u'v+ u',uv'=(uv) -u'v,[uv'dx = uv-Ju'vdx, [ udv=uv-f vdu.分部积分公式注：分部积分公式的作用：当左边的积分udv不易求得，而右边的积分vdu容易求得利用分部积分公式化难为易分部积分公式的关键：u和的选择

(uv) = uv + uv ,  uv (uv) − uv,   = uv dx uv u vdx,    = −  udv uv vdu.   = − 分部积分公式 一、基本内容 分部积分公式的关键: 注:分部积分公式的作用：当左边的积分 udv  不易求得，而右边的积分 vdu  容易求得 利用分部积分公式——化难为易 u v 和 的选择. 设函数u u x v v x = = ( ) ( ) 和 具有连续导数

二、例题例1 求积分xcosxdx.dr?令u=cosx,二解（一)= dyxdx :-21xI xcos xdxsin xdxcosx +22显然，u,v选择不当，积分更难进行解（二）令u=x，cosxdx=dsinx=dv[ xcos xdx= [ xd sin x= xsin x - [ sin xdx=xsinx+cosx+C

例1 求积分 cos .  x xdx 解（一） 令 u = cos x, xdx = dx = dv 2 2 1  xcos xdx  = + xdx x x x sin 2 cos 2 2 2 显然， u,v 选择不当，积分更难进行. 解（二） 令 u = x, cos xdx = d sin x = dv  xcos xdx  = xd sin x  = xsin x − sin xdx = xsin x + cos x + C. 二、例 题

综合：选择u后放的先后顺序，·反、对、幂、指、三

综合：选择u后放的先后顺序: • 反、对、幂、指、三

求积分[x"e*dx.例2解： u=x2,edx = de* = dv,[x'e*dx = [ x'de* = x'e* -2] xe*dx（再次使用分部积分法）u=x，e"dx=dy=+’e*-2] xde* = x’e* -2(xe* -e*)+C.总结若被积函数是幂函数和正(余)弦函数或幂函数和指数函数的乘积，就考虑设正(余)弦函数或指数函数为，而幂函数为u，使其降幂一次(假定幂指数是正整数

例2 求积分 . 2  x e dx x 解: , 2 u = x e dx de dv, x x = = 2 2 x x x e dx x de =   2 2 x x = − x e xe dx  2 2( ) . x x x = − − + x e xe e C （再次使用分部积分法） u = x, e dx dv x = 总结 若被积函数是幂函数和正(余)弦函数 或幂函数和指数函数的乘积, 就考虑设正 (余)弦函数或指数函数为 ，而幂函数 为 u , 使其降幂一次(假定幂指数是正整数) v  2 2 x x = − x e xde 

I xarctanxdx.例3求积分解： 令u=arctanx,dxdx == dv2x arctan xdx = [ arctan xd2X+d(arctanx)arctanx--2x-22x-2x-221一dxarctanx21+x(.(1)drarctanx(x -arctanx)+ C.arctanx-2

例3 求积分 arctan .  x xdx 解: 令 u = arctan x , dv x xdx = d = 2 2 2 arctan arctan 2 x x xdx xd =   (arctan ) 2 arctan 2 2 2 d x x x x  = − dx x x x x 2 2 2 1 1 2 arctan 2 + = −   dx x x x ) 1 1 (1 2 1 arctan 2 2 2 + = −  −  ( arctan ) . 2 1 arctan 2 2 x x x C x = − +

例4求积分「x"Inxdxx解:u=lnx, xdx=dd= dv4+[ x' In xdx = [ In xd4-x*In x -d+C一L16总结：若被积函数是幂函数和对数函数或幂函数和反三角函数的乘积，就考虑设幂函数为 ，而对数函数或反三角函数为 u

例4 求积分 ln . 3  x xdx 解: u = ln x, , 4 4 3 dv x x dx = d = 4 3 ln ln 4 x x xdx xd =   = x x − x dx 4 3 4 1 ln 4 1 . 16 1 ln 4 1 4 4 = x x − x + C 总结：若被积函数是幂函数和对数函数或幂 函数和反三角函数的乘积，就考虑设幂函数 为 v  ，而对数函数或反三角函数为 u

e* sin xdx.例5求积分-I sin xde*e"sinxdx解一:=e" sinx- {e"d(sinx)= e* sin x -[e* cosxdx = e* sinx - [cosxde'=e* sinx-(e* cosx-fe*dcosx)e"sinxdx=e"(sinx-cosx)注意循环形式ete* sin xdx=(sin x - cosx) +C.2

例5 求积分 sin .  e xdx x 解一：  e xdx x sin  = x sin xde  = e sin x − e d(sin x) x x  = e x − e xdx x x sin cos  = − x x e sin x cos xde  = e sin x − (e cos x − e d cos x) x x x  = e x − x − e xdx x x (sin cos ) sin  e xdx x sin (sin cos ) . 2 x x C e x = − + 注意循环形式

=-Je*d(cos x)e* sin xdx解二:= -e* cos x + [e* cos xdx= -e* cosx+ [e*d(sinx)注意循环形式e* sin xdx=-e* cosx+e*sinx-ete* sin xdx =(sinx-cosx)+C.2总结：若被积函数是正(余)弦函数和指数函数的乘积，原则上哪个作为或都可以，但注意要前后一致

解二： sin (cos ) x x e xdx e d x = −   cos cos x x = − + e x e xdx  cos (sin ) x x = − + e x e d x  cos sin sin x x x = − + − e x e x e xdx   e xdx x sin (sin cos ) . 2 x x C e x = − + 注 意 循 环 形 式 总结： 若被积函数是正(余)弦函数和指数函数的 乘积, 原则上哪个作为 或 都可以，但注意 要前后一致. v  u

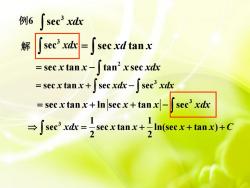
例6secxdxsec"xdx解= [ sec xd tan x= sec x tan x - [ tan’ x sec xdx= sec x tan x+ [ sec xdx -[ sec' xdxsecxdx= sec x tan x + In sec x + tan x-1→ sec' xdx == sec x tan x+=ln(sec x+tanx)+C22

例 6 3 sec xdx  解 3 sec xdx  = sec tan xd x  2 = − sec tan tan sec x x x xdx  3 = + − sec tan sec sec x x xdx xdx   3 = + + − sec tan ln sec tan sec x x x x xdx  3 1 1 sec sec tan ln(sec tan ) 2 2  = + + + xdx x x x x C 