《高等数学》课程教学资源（课件讲稿）第一章 函数与极限_1-7 无穷小比较

第七节无穷小的比较引例.x→0时,3x,x2,sin x都是无穷小,但sinxlimlim=03x3x→03xx-01sinxlimx-0可见无穷小趋于0的速度是多样的

x  0 时, 3 x , x , sin x 2 都是无穷小, 第七节 引例 . x x x 3 lim 2 0  0 , 2 0 sin lim x x x   , x x x 3 sin lim 0 , 3 1  但 可见无穷小趋于 0 的速度是多样的 . 无穷小的比较

定义.设α，β是自变量同一变化过程中的无穷小若 limB=0,则称β是比α高阶的无穷小,记作αβ = o(α)nB=,则称 β是比α 低阶的无穷小;若limα,B=C0， 则称β是α 的同阶无穷小;若limαβ若lim=C±0.则称β是关于α的k阶无穷小kd若 limB=1,则称 β是α 的等价无穷小,记作α~βa或β~α

lim  C  0, k   定义. lim  0,  若  则称  是比  高阶的无穷小,   o( ) lim  ,   若 若 若 lim 1,   若  ~   ~  lim  C  0,   或 设  ,  是自变量同一变化过程中的无穷小, 记作 则称  是比  低阶的无穷小; 则称  是  的同阶无穷小; 则称  是关于  的 k 阶无穷小; 则称  是  的等价无穷小, 记作

例如，当x→0 时x3=o(6x2); sinx～x; tanx～xarcsinx~x又如，2sin1-cosxlim=lim4()2x-0x-0故x→0时1-cosx是关于x的二阶无穷小，且1 - cos x~

例如 , 当  o( ) ～ x  0 时 3 x 2 6x ; sin x x ; tan x ～ x arcsin x ～ x 2 0 1 cos lim x x x   2 2 0 2sin lim x x  又如 ， 2 2 4( ) x 2 1  故 时 是关于 x 的二阶无穷小, 1  cos x 2 2 1 ～ x 且

例1.证明：当x→0时,1+x-1～=,nn/1+x-1证：lim1xx-0a" -b" = (a-b) (an-l +an-2b +...+bn-l)分子=x(n/1+x)-1= limx-01x [("1+x y~- +(°/1+x )~-2 +..+1]:.当x→0时, n/1+x-1～n

例1. 证明: 当 时, ～ 证: ～   n n a b (a  b) 1 ( n a a b n2  ) 1   n  b

例2.证明：e-1~x.证：令=e-1,则x=ln(1+y),且x→0时,→0因此Llimlimlimy=0 1 In(1+ y)y→>o ln(1 + y)-0x1= limIney→0 ln(1 + y)即有等价关系：e-1~x说明：上述证明过程也给出了等价关系In(1 +x) ~ x

例2. 证明: 证: 因此 即有等价关系: 说明: 上述证明过程也给出了等价关系:

常用等价无穷小：当x→0时sinx~x,arcsinx~x,tanx~x,arctanx~x,In(1+x)~ x, e*-l~ x, 1-cosx2+x-1~*1+x-1~=x,n(1+x)α-1~ax说明：1.上述10个等价无穷小必须熟练掌握2.将x换成Vo(x）→0都成立

常用等价无穷小: 当x 0 , 时 2 sin ~ , arcsin ~ , tan ~ , arctan ~ , 1 ln(1 ) ~ , 1 ~ , 1 cos ~ , 2 x x x x x x x x x    x x e x x x 1 1 1 ~ , 2   x x 1 1 1 ~ , n x x n   (1 ) 1~ α   x αx 说明： 1. 上述10个等价无穷小必须熟练掌握 2. ( ) 0 将x换成  φ x 都成立

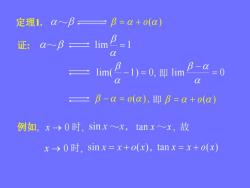
定理1. α～ββ=α+o(α)B证： α～βlim3β-αP-1)= 0, 即 lim=0limaαβ-α=o(α),即β=α+o(α)I例如，x→o时，sinx～x，tan x～x，故x→0时, sinx=x+o(x), tan x= x+o(x)

～ ～ 定理1.     o( ) 证: lim  1   lim( 1)  0,   lim  0     即     o( ), 即     o( ) 例如, x  0 时, ～ tan x ～ x , 故 x  0 时, tan x  x  o( x)

B定理2.设 α~α',β~β,且 lim存在，则aβBlim= limQaBβB证：1lim:limBaβBBdlimlim= limlimβQQatan2x2X: lim例如，lim5x-05xx→0sin5x

定理2 . 设 且 存在 , 则   lim 证:   lim           lim           lim     lim   lim      lim 例如, x x x sin 5 tan 2 lim 0 x x x 5 2 lim 0  5 2 

说明：设对同一变化过程，α，β为无穷小，由等价无穷小的性质，可得简化某些极限运算注意：1、乘积项等价无穷小放心用：若α～β,且 β(x)极限存在或有界,则lim αo(x) =lim βp(x)例如，lim arcsin x·sin== lim x·sin== 0x-0xx0x2、和差项等价无穷小需谨慎：

说明: 设对同一变化过程 ,  ,  为无穷小 , 无穷小的性质, 由等价 可得简化某些极限运算. 1、乘积项等价无穷小放心用： 若  ~  , 且  ( x) 极限存在或有 界, 则 lim  ( x)  lim  ( x) 例如, 0 1 lim sin 1 lim arcsin sin 0 0       x x x x x x 2、和差项等价无穷小需谨慎： 注意:

2、和差项等价无穷小需谨慎：(1)和差取大规则：若β=o(α)，则α±β～αx 1sinx= lim =例如，limx→0 x3 +3x~ x→03x- 3(2)和差代替规则：若 α～α,β～β'且 β与α不等价α-βα'-β"则 α- β~α'-β', 且 limimy2x-xtan2x-sinx例如，lim:limx-→0 /1+x-1x-0注意α～β时需将α-β化成等价的形式再计算

(1) 和差取大规则: 若  = o() , (2) 和差代替规则: 若 α ~ , ~ , α   β β 且 β 与 α 不 等 价 则   ~      , 例如, x x x x 3 sin lim 3 0  x x x 3 lim 0  3 1  则   ~  lim lim .            且 注意 α ~ β 时需将α-β化成等价的形式再计算。 例如, 1 1 tan 2 sin lim 0     x x x x x x x x 2 1 0 2 lim     2 2、和差项等价无穷小需谨慎：