《高等数学》课程教学资源（课件讲稿）第四章 不定积分_4-4 有理函数的积分

第四节第四章有理函数的积分·基本积分法：直接积分法：换元积分法；分部积分法求导·初等函数初等函数积分本节内容：一、有理函数的积分二、可化为有理函数的积分举例

第四节 • 基本积分法 : 换元积分法 ; 分部积分法 • 初等函数 求导 初等函数 积分 一、有理函数的积分 二、可化为有理函数的积分举例 有理函数的积分 本节内容: 第四章 直接积分法 ;

一、有理函数的积分有理函数：n-1aox"+aix"1+...+anP(x)R(x) =Q(x)boxm +bixm-1 +...+ bmm≤n时,R(x)为假分式;m>n 时,R(x)为真分式有理函数真分式多项式+相除分解若干部分分式之和其中部分分式的形式为AMx+N(kEN+,p2-4q<0)(x-a)k"(x2+px+q)

一、 有理函数的积分 ( ) ( ) ( ) Q x P x R x   n n n a x  a x   a 0 1 1  有理函数: m  n 时, 为假分式; m  n 时, 为真分式 有理函数 相除 多项式 + 真分式 分解 其中部分分式的形式为 k k x p x q M x N x a A ( ) ; ( ) 2     ( , 4 0 ) 2     k N p q 若干部分分式之和

有理函数化为部分分式之和的一般规律：（1）分母中若有因式（x-α)k，则分解后为AR(x-a)k(x-a)kx-a其中A,AA是常数如：x-3x-3(x-1)(x2 -1)(x -1)(x+1)B(x-1)2x-1x+1

有理函数化为部分分式之和的一般规律： （1）分母中若有因式 ( ) x a  k ，则分解后为 1 2 1 , ( ) ( ) k k k A A A x a x a x a        1 2 , , , . 其中A A Ak 是常数 如： 2 3 ( 1)( 1) x x x    2 3 ( 1) ( 1) x x x    2 ( 1) 1 A B x x     1 D x  

(2）分母中若有因式（x2+px+g)，其中p2-4q<0则分解后为M,x+NM,x+N,M,x+N(x? + px+g)*+ (x? + px+g)k-x?+px+q其中M,N(i=lk)都是常数

（2）分母中若有因式 ( ) x px q 2   k ，其中 则分解后为 2 p q   4 0 1 1 2 2 2 2 1 2 ( ) ( ) k k k k M x N M x N M x N x px q x px q x px q              , ( 1, , ) 其中M N i k i i  都是常数

四种典型部分分式的积分：dx=Aln x-a+C(x-a)l-n +C (n±l)Ya(x2+ px+q)Mx+N=2x+p3dx变分子为x?+ px+q(2x+ p) +N_MpMx+Ndx再分项积分(x? + px +q)n(p2-4g<0,n±1)

四种典型部分分式的积分:  Aln x  a  C x a C (n  1) n A n     1 ( ) 1   x x a A 1. d   x x a A n d ( ) 2.     x x px q M x N 3. d 2     x x px q M x N n d ( ) 4. 2 变分子为 (2 ) 2 x p M  2 M p  N  再分项积分 x p x px q      2 ( ) 2

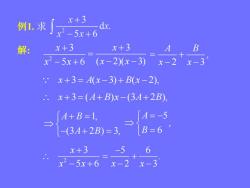
x+3dx.例1.求x2-5x+6x+3x+3BA解：x2-5x+6 (x-2)(x-3) x-2x-3x+3= A(x-3)+B(x-2)x+3=(A+B)x-(3A+2B)A=-5A+B=1B=6-(3A+2B) = 3,x+36x2-5x+6 x-2x-3

例1. 求 解: 2 3 5 6 x x x    3 ( 2)( 3) x x x     , 2 3 A B x x     x A x B x      3 ( 3) ( 2),       x A B x A B 3 ( ) (3 2 ), 1, (3 2 ) 3, A B A B          5 , 6 A B        2 3 5 6 x x x     5 6 . x x 2 3     

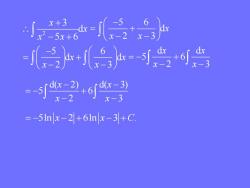
x+3dx:dx-5x+6x-2x-dx++6dx=一r d(x-3) d(x-2)-57+6?x-2x-3=-5lnx-2+6lnx-3+C

2 3 d 5 6 x x x x      5 6 d 2 3 x x x             5 6 d d 2 3 x x x x                    d d 5 6 2 3 x x x x        d( 2) d( 3) 5 6 2 3 x x x x                5ln 2 6ln 3 . x x C

x+2dx.例2.求(2x+1)(x2+x+1)x+2ABx+D解：x?+x+1(2x+1)(x2 + x+1)2x+1x+2: A=(2x+1)·原式=2X=x+x+1分别令x=0,1代入等式两端2=2+DB=-132B+DD=0→O32x+2x(2x+1)(x2+x+l) 2x+1 x2+x+1

例2. 求 解: 2 2 (2 1)( 1) x x x x     2 1 A x   2 1 Bx D x x         A x (2 1) 原式 1 2 x   2 1 2 2 1 x x x x        2 2 2   D 3 2 9 3 3 B D   B  1 D  0 2 2 (2 1)( 1) x x x x      2 2 1 x   2 1 x x x   

2x+2xdxdx =2x+1-x?+x+1(2x+1)(x2 +x+1)Xdx-dx2x+1+x+1「=(x? +x+1)-}d(2x+1)dxx2+x+12x+1dx-+x+1小dx=In|2x+1-=In(x? +x+1)++（+）2x+1= In|2x+1 -=1n(x2 +x+1) +CarctanV3/3

2 2 d (2 1)( 1) x x x x x      2 2 d 2 1 1 x x x x x             2 2 d d 2 1 1 x x x x x x        d(2 1) 2 1 x x     2 2 ( 1) d 1 x x x x x        1 2 1 2 -   ln 2 1 x 2 2 1 d( 1) 2 1 x x x x       2 1 d 2 1 x x x       ln 2 1 x 1 2 ln( 1) 2    x x   2 1 3 2 4 1 d 2 x x       ln 2 1 x 1 2 ln( 1) 2    x x 1 2 1 arctan . 3 3 x C   

x-3dx例3.求(x -1)(x2 -1)Bx-3Dx-3解：(x-1)(x2-1)(x-1)(x+1)(x-1)x-1x+1x-3：D=(x+1)·原式一X二(x-1)X=-分别令x=0,2代入等式两端-3=A-B-1A=-1大B=13I1x-3x+1(x-1)(x2 -1)(x-1)x-1

例3. 求 解: 2 3 ( 1)( 1) x x x    2 3 ( 1) ( 1) x x x     2 ( 1) 1 1 A B D x x x           D x( 1) 原式 x  1 2 3 ( 1) 1 x x x       1     3 1 A B 1 1 3 3     A B A  1 B 1 2 3 ( 1)( 1) x x x     2 1 1 1 ( 1) 1 1 x x x       