《高等数学》课程教学资源（课件讲稿）第七章 微分方程_7-5 可降阶高阶微分方程

第七章第五节可降阶高阶微分方程一、 (n) = f(x)型的微分方程二、"=f(x,)型的微分方程三、J"=f(y,J)型的微分方程

可降阶高阶微分方程 第五节 一、 型的微分方程 二、 型的微分方程 三、 型的微分方程 第七章

一、y(n)= f(x)型的微分方程令==(-1),则=(m)=f(x),因此dxz =[ f(x)dx+Ci即J(n-1) = [ f(x)dx+C同理可得 y(n-2) =[[J f(x) dx+C, Jdx+C2= JJ f(x)dx Jdx +Cix+C2依次通过n次积分，可得含n个任意常数的通解

一、 ( ) ( ) y f x n  令 , ( 1)  n z y 因此 1 z   f (x)dx  C 即 同理可得   2 ( 2) y dx C n      dx   依次通过 n 次积分, 可得含 n 个任意常数的通解 . 1 C2  C x  型的微分方程

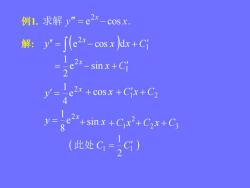
例1.求解 y" =e2x-cos x.解: y"= [(e2x-cos x)dx+Ci- sin x + Ci2x +cos x +Cx+C2+ sin x + Cix?+C2x + C38(此处Ci=Ci)

例1. 解:   1 2 y e cos x dx C x       1 2 e sin 21 x C x     x y 2 e 41   x y 2 e 81   sin x 2 1  C x 2 C3  C x   cos x 1 C2  Cx 

二、"=f(x,y）型的微分方程设 y'=p(x),则y"=p,原方程化为一阶方程p'= f(x, p)设其通解为寸p=β(x,C)则得y' = β(x,C)再一次积分，得原方程的通解y= [p(x,Ci)dx+C2

y   f (x, y ) 型的微分方程 设 y   p (x) , 原方程化为一阶方程 设其通解为 ( , ) C1 p   x 则得 ( , ) C1 y    x 再一次积分, 得原方程的通解 1 2 y   (x,C )dx  C 二

[(1+x2)y"=2xy'例2.求解Jx=0 =1，|x=0=3解：设 '= p(x),则y"= p',代入方程得dp2xdx分离变量(1 +x2)p' = 2xpp(1+x2)积分得 Inp|=ln(1+x2)+lnlC l,即p=C(1+x2)利用 |x=0 =3,得 Ci=3,于是有 y'=3(1+x2)两端再积分得=x3+3x+C2利用 |x=0 =1,得 C2 =1,因此所求特解为y=x3 +3x+1

例2. 求解 (1 x )y   2xy  2 1, y x 0  3 y  x 0  解: 代入方程得 (1 x )p 2x p 2    分离变量 积分得 ln ln (1 ) ln , 1 2 p   x  C 3 , 利用 y  x 0  3, 得 C1  于是有 3(1 ) 2 y    x 两端再积分得 2 3 y  x  3 x  C 利用 1, y x 0  1, 得 C2  3 1 3 y  x  x  因此所求特解为

三、y"=f(y,y)型的微分方程dp- dp.dydp2令y'= p(y), 则y"=dydxdy dxdp = f(y,p)故方程化为di设其通解为 p=β(y,C),即得y'= (y,C)分离变量后积分，得原方程的通解dy=x+Cp (y,C)

三、 y   f ( y, y ) 型的微分方程 令 y   p ( y), x p y d d 则   x y y p d d d d   故方程化为 设其通解为 ( , ), C1 p   y 即得 分离变量后积分, 得原方程的通解

例3. 求解 yy"-y= 0解:设y'=p(y),则y"==dydppdydxdydxdp_ dydp2=0,即n代入方程得yp福dyyp两端积分得Inpl=Iny+lnCil，即p=CiyJ'=Ciy(一阶线性齐次方程)故所求通解为 =CzeCix

例3. 求解 代入方程得 两端积分得 ln ln ln , C1 p  y  , 1 即 p  C y (一阶线性齐次方程) 故所求通解为 解: x p y d d 则   x y y p d d d d  y p p d d 

[y"-e2y =0例4.解初值问题(|x=0 =0, 'x=0 =1dp,代入方程得解:令=p(v),则=%pdp=e?'dy积分得2p? =e2+Ci利用初始条件,得Ci =0,根据 ply=0=ylx=0 =1>0,得=p=eydx积分得 -e-= x+C2,再由ylx=0 =0,得C2=-11-e-y =x故所求特解为

例4. 解初值问题 解: 令    e 0 2    y y 0 , y x 0  1 y  x 0  y   p ( y), , d d y p 则 y   p 代入方程得 积分得 1 2 2 2 1 2 1 p e C y   利用初始条件, 1 0, 0, p y0 y  x0   得C1  根据 y p x y e d   d 积分得 e , C2 x y     0, 再由y x0  1 得C2   故所求特解为 x y    1 e 得

内容小结法一降阶法可降阶微分方程的解法1. y(n) = f(x)逐次积分2. y"= f(x,y')令'=p(x),则"=dpdx3. y"= f(y,y')dp令y'= p(y), 则y"= pdy

内容小结 可降阶微分方程的解法 —— 降阶法 逐次积分 令 y   p(x) , 令 y   p( y)

作业P3291 (3),(5), (7) , (10) ;2 (3), (6) ;

P329 1 (3) ,(5), (7) , (10) ; 2 (3) , (6) ; 作业