《高等数学》课程教学资源（课件讲稿）第五章课件_第五章第4节定积分的应用

第五章第四节定积分的应用微元法一、二、定积分在几何上的应用平面图形的面积2、体积3、平面曲线的弧长HIGH EDUCATION PRESS机动目录上页下页返回结束

第四节 机动 目录 上页 下页 返回 结束 定积分的应用 一、微元法 第五章 二、定积分在几何上的应用 1、平面图形的面积 2、体积 3、平面曲线的弧长

微元法一、1、什么问题可以用定积分解决？1) 所求量 U 是与区间[α,b]上的某分布,f(x) 有关的一个整体量；2）U对区间[α，bl具有可加性，即可通过“大化小，常代变，近似和，耳取极限”n表示为ZJU = limf(5)Ax;1-0i-1n-bZ定积分定义:limf(x)dx=f(S)Axid20i-lHIGHEDUCATIONPRESS机动目录上页下页返回结束

表示为 1、什么问题可以用定积分解决 ? 1) 所求量 U 是与区间[a , b]上的某分布 f (x) 有关的 2) U 对区间 [a , b] 具有可加性 , 即可通过 “大化小, 常代变, 近似和, 取极限” 定积分定义 机动 目录 上页 下页 返回 结束 一个整体量 ; 一、微元法

如何应用定积分解决问题？2..第一步利用求出局部量"化整为零，以常代变微分表达式的近似值dU = f(x)dx第二步求出整体量利用“积零为整，无限累加的精确值积分表达式bJ=f(x)dx天（或微元分析法）这种分析方法成为元素法HIGH EDUCATION PRESS第二节目录上页返回结束下页

2、如何应用定积分解决问题 ? 第一步 利用“化整为零 , 以常代变” 求出局部量 微分表达式 dU = f (x) dx 第二步 利用“ 积零为整 , 无限累加 ” 求出整体量 积分表达式 U = f x x b a ( ) d  这种分析方法成为元素法 (或微元分析法) 的近似值 的精确值 第二节 目录 上页 下页 返回 结束

二、定积分在几何上的应用1、平面图形的面积HIGH EDUCATION PRESS

二、定积分在几何上的应用 1、平面图形的面积

1.直角坐标情形yt y= f(x)设曲线 y=f(x)(≥0)与直线x=aα,x=b(a<b)及x轴所围曲oaxibx边梯形面积为A，x+dxdA= f(x)dxf(x)dxHIGH EDUCATION PRESS机动目录上页下页返回结束

1. 直角坐标情形 设曲线 与直线 及 x 轴所围曲 dA = f (x) dx o a b x y y = f (x) x x + dx A f x x b a ( )d  = 机动 目录 上页 下页 返回 结束 边梯形面积为 A

设曲线 y=f(α)，y= f,(x)yty= fi(x) y= f2(x)与直线 x=α,x=b(a<b)及x轴所围曲边梯形面积为Abxaxx+dxdA =fi(x)- f2(x)|dxA= (lfi(x) - f2(x) dxHIGH EDUCATION PRESS机动目录上页下页返回结束

1 2 d ( ) ( ) d A f x f x x = − 机动 目录 上页 下页 返回 结束 y o a b x ( ) 2 ( ) y = f x 1 y = f x A f x f x x b a ( ) ( ) d =  1 − 2 x x + d x 设曲线 与直线 及 x 轴所围曲边梯形面积为 A

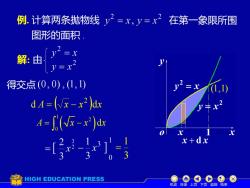
例.计算两条抛物线y?=x, y=x在第一象限所围图形的面积解:由得交点(0,0)，（1,1)T1(1.1)d A= (/x-x2)dxH店A= J(V-x)dxxx+dxHIGH EDUCATION PRESS机动目录上页下页返回结束

例. 计算两条抛物线 在第一象限所围 图形的面积 . x y = x 2 o y 2 y = x x x + d x 解: 由 得交点 (0, 0) , (1, 1) (1,1) 1 d A ( x x )dx 2 = − 3 1 = 机动 目录 上页 下页 返回 结束 ( ) 1 2 0 A x x x = − d 

2=2x与直线 =x-4所围图形例.计算抛物线的面积=2x得交点解:由2xy=x-4(8,4)0+(2, -2),(8,4)为简便计算，选取y作积分变量x=x-4则有(y+4-{y)d)=[2+4y-3 ]-2=18HIGH EDUCATION PRESS机动目录上页下页返回结束

x y 2x 2 = o y y = x − 4 例. 计算抛物线 y 2x 2 = 与直线 的面积 . 解: 由 得交点 (2, − 2) , (8, 4) (8, 4) d A ( y 4 y )dy 2 2 1 = + − = 18 y = x − 4 所围图形 (2,− 2) 为简便计算, 选取 y 作积分变量, 则有 y y + d y −  = 4 2 A 机动 目录 上页 下页 返回 结束

例.求椭圆所围图形的面积解：dA=ydxOydxA=4xx+dxa x利用椭圆的参数方程x= acost(0≤t≤2元)y=bsint应用定积分换元法得2bsint ·(-asint)dt = 4abtdtsin20元2=4αb.1.=πab当α=b时得圆面积公式2.2HIGH EDUCATION PRESS机动目录上页下页返回结束

a b o x y x 例. 求椭圆 解: d A = y dx 所围图形的面积 .  = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos       = = t y b t x a t 应用定积分换元法得  = 2 0 2 4 sin d  ab t t = 4ab 2 1  2   =  ab 当 a = b 时得圆面积公式 机动 目录 上页 下页 返回 结束 x + d x

2.极坐标情形设β(の)C[α,β], β(O)≥0, 求由曲线 r =(0) 及射线=α,θ=β围成的曲边扇形的面积在区间[α,β]上任取小区间[,+dθ]则对应该小区间上曲边扇形面积的近似值为@(0)[o(0)]2 dedA=de所求曲边扇形的面积为0@"(0)deaxHIGH EDUCATION PRESS机动目录上页下页返回结束

2. 极坐标情形 求由曲线 及 围成的曲边扇形的面积 . r = ( )  x  d 在区间 上任取小区间 则对应该小区间上曲边扇形面积的近似值为 ( ) d 2 1 d 2 A = 所求曲边扇形的面积为      ( )d 2 1 2  A = 机动 目录 上页 下页 返回 结束 