《高等数学》课程教学资源（课件讲稿）第五章课件_第5章第1节 定积分的概念及性质

第五章第一节定积分的概念及性质实际问题二、定积分的定义三、定积分的性质HIGH EDUCATION PRESS机动目录上页下页返回结束

第一节 一、实际问题 二、 定积分的定义 三、 定积分的性质 机动 目录 上页 下页 返回 结束 定积分的概念及性质 第五章

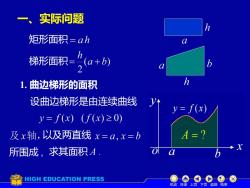
一、实际问题矩形面积=ah梯形面积=(a+b)bh1.曲边梯形的面积设曲边梯形是由连续曲线Vy= f(x)y=f(x) (f(x)≥0)A=?及x轴，以及两直线x=a,x=b0所围成，求其面积Aa福HIGH EDUCATION PRESS机动目录上页下页返回结束

一、实际问题 1. 曲边梯形的面积 设曲边梯形是由连续曲线 以及两直线 所围成 , 求其面积 A . A = ? 机动 目录 上页 下页 返回 结束 y = f ( x) 矩形面积 梯形面积

解决步骤：1) 分割在区间[α，b]中任意插入n-1个分点a = Xo <Xi < X2 <...<Xn-1 < Xn = b用直线x=x;将曲边梯形分成n个小曲边梯形2）近似在第i个窄曲边梯形上任取SiE[xi-1,xi]V作以[xi-1,x,]为底，f(5)并以此小为高的小矩形梯形面积近似代替相应olaxjbxXi-1 Xi△Ai,得窄曲边梯形面积5iA, = f(S)△xi(xi = x; -xi-1, i=1,2,..,nHIGH EDUCATION PRESS机动目录上页下页返回结束

1 x i x i−1 a x y o 解决步骤 : 1) 分割. 在区间 [a , b] 中任意插入 n –1 个分点 a x x x x x b = 0  1  2   n−1  n = [ , ] i i 1 i x x  −  用直线 i x = x 将曲边梯形分成 n 个小曲边梯形; 2) 近似. 在第i 个窄曲边梯形上任取 作以 [ , ] i 1 i x x − 为底 , ( ) i f  为高的小矩形, 并以此小 梯形面积近似代替相应 窄曲边梯形面积 得 ( ) ( )  i  i  i  i = i − i−1 A f  x x x x  i 机动 目录 上页 下页 返回 结束

3)求和nnA=ZA; ~Zf(E)Axii=1i=14)取极限令 =max{△x;},则曲边梯形面积<i<nnZA= limA;20i=1nE.lim(E)△xi1-0i-1OabxXiXi-1 XiSHIGH EDUCATION PRESS机动目录上页下页返回结束

3) 求和.  = =  n i A Ai 1  =   n i i i f x 1 ( ) 4) 取极限. 令 则曲边梯形面积  → = =  n i A Ai 1 0 lim   → = =  n i i i f x 1 0 lim ( )  机动 目录 上页 下页 返回 结束 a y o 1 x i x i−1 x  i

2.变速直线运动的路程设某物体作直线运动已知速度 v=v(t) eC[Ti, T], 且v(t)≥0,求在运动时间内物体所经过的路程 s.解决步骤：1) 分割在[Ti,T2]中任意插入 n-1个分点,将它分成n 个小段[ti-1,t;](i=1,2,,n),在每个小段上物体经过的路程为 △si(i=l,2,., n)2)近似任取5;ε[ti-1,ti],以v(s;)代替变速，得△ s; = v(S)△t;(i=l, 2,.,n)HIGH EDUCATIONPRESS机动目录上页下页返回结束

2. 变速直线运动的路程 设某物体作直线运动, 且 求在运动时间内物体所经过的路程 s. 解决步骤: 1) 分割. 将它分成 在每个小段上物体经 2) 近似. 得 i i i  s  v( )t (i = 1, 2,  ,n) 已知速度 机动 目录 上页 下页 返回 结束 n 个小段 过的路程为

3)求和Vv(5i)△t;>i-14)取极限ns = lim(a = max △t)v(S)△ti1>0<i<nilHIGH EDUCATION PRESS目录机动上页下页返回结束

3) 求和. 4) 取极限 . 机动 目录 上页 下页 返回 结束

二、定积分定义设函数,f(x)定义在[a,b]上,若对[a,b]的任一种分法α= xo <Xi <x2<...<Xn =b, 令△x;= X; -xi-1,任取nZ f(5)△xi5;E[xi,Xi-1],只要几= max{△x;}→0时l<i<ni=1总趋于确定的极限I,则称此极限I为函数f(x）在区间rb记作[a,b]上的定积分f(x)dx-nα xixi-ix, b xbZf(5i)Axi即limf(x)dx = I101i=1此时称f（x）在［α,b］上可积HIGH EDUCATION PRESS机动目录上页下页返回结束

o a b x 二、定积分定义 任一种分法 , 0 1 2 a x x x x b =     n = 任取  i 总趋于确定的极限 I , 则称此极限 I 为函数 在区间 上的定积分, 1 x i x i−1 x  b a f (x)dx 即 =  b a f (x) dx i n i i  f x → =1 0 lim ( )  此时称 f ( x ) 在 [ a , b ] 上可积 . 记作 机动 目录 上页 下页 返回 结束

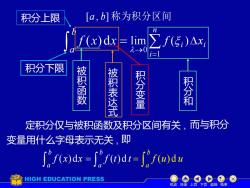
[α,b]称为积分区间积分上限nZJf(x)dx= limf(E)Axi1-0i=1积分下限被积函数被积表达式积分变量积分和定积分仅与被积函数及积分区间有关，而与积分变量用什么字母表示无关，即af(x)dx =f(t)dt=f(u)duCHIGHEDUCATIONPRESS机动目录上页下页返回结束

=  b a f (x)dx i n i i  f x = → 1 0 lim ( )  积分上限 积分下限 被 积 函 数 被 积 表 达 式 积 分 变 量 积 分 和 [a , b] 称为积分区间 定积分仅与被积函数及积分区间有关 , 而与积分 变量用什么字母表示无关 , 即  b a f (x)dx  = b a f (t)d t  = b a f (u)d u 机动 目录 上页 下页 返回 结束

定积分存在的充分条件若函数 f(x)在闭区间[a,b] 上连续1.则函数(x)在闭区间[a,b] 上可积2.若函数 f(x)在闭区间[α,b] 上除有限个第一类间断点外处处连续，则函数f(x)在闭区间[α，b] 上可积HIGH EDUCATION PRESS

定积分存在的充分条件 在 闭区间[a , b] 上连续 在闭区间[a , b] 上可积 1. 2. 在 闭区间[a , b] 上除有限个 第一类间断点外处处连续， 在闭区间[a , b] 上可积

定积分的几何意义：曲边梯形面积Tf(x)dx= Af(x)>0,曲边梯形面积的负值Tf(x)dx =-Af(x)<0,A5A2bx福~f(x)dx = Ai - A2 + As - A4 + As各部分面积的代数和HIGH EDUCATION PRESS机动目录上页下页返回结束

定积分的几何意义: 曲边梯形面积 曲边梯形面积的负值 a b y x A1 A2 A3 A4 A5 1 2 3 4 5 f (x) d x A A A A A b a = − + − +  各部分面积的代数和 机动 目录 上页 下页 返回 结束