《高等数学》课程教学资源（课件讲稿）第六章 定积分的应用_6-2 定积分在几何学上的应用

第六章第二节定积分在几何学上的应用平面图形的面积二、体积三、平面曲线的弧长

二、体积 第二节 一、 平面图形的面积 三、 平面曲线的弧长 定积分在几何学上的应用 第六章

一、平面图形的面积1.直角坐标情形设曲线y=f(x)(≥0)与直线yt y= f(x)x=a,x=b（a<b）及x轴所围曲边梯形面积为A，则dA = f(x)dxOaxbxx+dxA= J" f(x)dx

一、平面图形的面积 1. 直角坐标情形 设曲线 与直线 及 x 轴所围曲 则 dA  f ( x) dx A f x x b a ( ) d   边梯形面积为 A , O a b x y y  f ( x ) x  dx x

例1.计算两条抛物线2=x,=x2在第一象限所围图形的面积解：由得交点（0,0），（1,1)y2 =x (1,1)A=(Vx-x2)dxAx+dx

例1. 计算两条抛物线 在第一象限所围 图形的面积 . 解: 由 得交点 (0 , 0) , (1, 1) d A ( x x ) dx 2   3 1     1 0 A x y O y  x 2 2 y  x x x  d x (1,1) 1

例2.计算抛物线y2=2x与直线y=x-4所围图形的面积=2x得交点解：由y2 = 2x8,4)y=x-4V+((2, -2), (8, 4)为简便计算，选取V作积分变量?=x-4则有2.-[, (y+ 4-1y2)dyA=I=[22 +4y-13 ]42 = 18

O y 2x 2  y  x  4 x y 例2. 计算抛物线 y 2x 2  与直线 的面积 . 解: 由 得交点 (2 ,  2) , (8 , 4) (8 , 4) d A ( y 4 y ) d y 2 2 1     18 y  x  4 所围图形 (2 ,  2) 为简便计算, 选取 y 作积分变量, 则有    4 2 A y y  d y

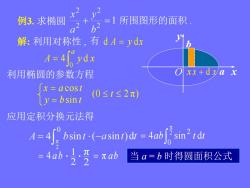
=1所围图形的面积例3.求椭圆6V解：利用对称性，有 dA=ydxA= 4fydxxx+dxax利用椭圆的参数方程x=acost(0≤t≤2元）y=bsint应用定积分换元法得sin'tdtbsint (-asint)dt = 4ab=4ab.1.元=元ab当a=b时得圆面积公式22

a b 例3. 求椭圆 解: 利用对称性 , d A  y dx 所围图形的面积 . 有   a A y x 0 4 d 利用椭圆的参数方程 (0 2 π ) sin cos     t y b t x a t 应用定积分换元法得   2 π 0 2 4ab sin t dt  4 ab 2 1  2 π   π ab 当 a = b 时得圆面积公式 x x  d x x y O

2.极坐标情形设p(0)C[α,β], (0)≥0, 求由曲线 r=β(0) 及射线θ=α,θ=β围成的曲边扇形的面积在区间[α，β]上任取小区间[0,0+dの]则对应该小区间上曲边扇形面积的近似值为p(0)dA =_[(0)]2 dde所求曲边扇形的面积为30[2(0)deQx

2. 极坐标情形 求由曲线 及 围成的曲边扇形的面积 . r   ( )   d 在区间 上任取小区间 则对应该小区间上曲边扇形面积的近似值为  ( ) d 2 1 d 2 A  所求曲边扇形的面积为      ( ) d 2 1 2  A   O x

例4.计算阿基米德螺线r=α0（α>0)对应θ从0变到2元所围图形面积2元a解: A = ["(a ) doXde2元[0]

例4. 计算阿基米德螺线 对应  从 0 变 解:  d (  ) d 2 1 2 a   2π 0 A 2 2 a        3 3 1  0 2π 3 2 π 3 4  a 到 2 所围图形面积 . 2 π a O x 阿基米德

例5.计算心形线r=a(1+cosの）（a>0）所围图形的心形线面积(1 + coso)? do（利用对称性）解：A=福40deα4cosde2令=2a x=8α2[cosAtdt031元3=8a元a4 2 22勒内·第卡尔克里新门

O 2a x 8a cos t dt 2 π 0 2 4   例5. 计算心形线 所围图形的 面积 . 解:  d (1 cos ) d 2 1 2 2 a    π 0 2 a   d 2 4 cos 4 (利用对称性) 2  令 t    2 8a  4 3  2 1 2 π 2 π 2 3  a 心形线 勒内·笛卡尔 克里斯汀

例6.计算心形线r=a(l+cosの）（a>0)与圆r=a所围图形的面积解：利用对称性，所求面积元(1+coso)de元0儿12cos0+=cos20)d0+元22二元-2a2ax元

  2 1  2 cos  cos (1 cos 2 ) 2 1   a 2a x y O 例6. 计算心形线 与圆 所围图形的面积 . 解: 利用对称性 , 所求面积 (1 cos ) d 2 1 2 2    2 a 2 π 2 1 A  a    2 2 π 2 1 a a  cos 2 ) d 2 1 2 cos 2 3 (    π 2  4 3 π 2 1 2 2  a  a 

二、 体积1.旋转体的体积旋转体就是由一个平面图形绕这平面内一条直线旋转一周而成的立体。这直线叫旋转轴特别，当考虑连续曲线段y=f(x）（α≤x≤b)绕x轴轴旋转一周围成的立体体积时，有y= f(x)V元[f(x)]?dxbXx

特别 , 当考虑连续曲线段 2 π[ f ( x)] 轴旋转一周围成的立体体积时, 有 dx   b a V x y a b x y O a b y  f ( x ) x 二、体积 1. 旋转体的体积 旋转体就是由一个平面图形绕这平面内一条直线旋转 一周而成的立体。这直线叫旋转轴