《高等数学》课程教学资源（课件讲稿）第二章 导数与微分_2-3 高阶导数

第三节高阶导数一、高阶导数的概念二、高阶导数的运算法则

二、高阶导数的运算法则 第三节 一、高阶导数的概念 高阶导数

一、高阶导数的概念引例：变速直线运动s=s(t)ds速度即=sVdtdv加速度dtd即a=(s')

一、高阶导数的概念 速度 即 v  s  加速度 即 a  (s ) 引例：变速直线运动

定义.若函数y=f(x)的导数y=f(x)可导，则称dV，即f(x）的导数为f(x）的二阶导数，记作y"或dx2或y"=(y)类似地，二阶导数的导数称为三阶导数，依次类推n-1阶导数的导数称为n阶导数，分别记作（n)1（4y".d'ydnyd4y或dx3dxndx

定义. 若函数 y  f (x) 的导数 y   f ( x) 可导, 或 即 y   ( y ) 或 ) d d ( d d d d 2 2 x y x x y  类似地 , 二阶导数的导数称为三阶导数 , n  1 阶导数的导数称为 n 阶导数 , 或 的导数为 f (x) 的二阶导数 , 记作 依次类推 , 分别记作 则称

例1. 设 y=ao +ax+a2x? +..+a,x",求 y(n)解:y'=a +2azx+ 3agx? + ..+ nanxn-ly" = 2 .la2 + 3. 2ax +.. + n(n -1)a,xn-2依次类推，可得y(n) = n!an思考：设=x（μ为任意常数）,问(n）=？(x")(m) = μ(μ- 1)(μ- 2)...(μ- n + 1)xu-n

设 求 解: y   a1  2a2 x  1  n n  na x y   2 1a2  a x3 3  2 2 ( 1)     n n  n n a x 依次类推 , n n y n!a ( )   2 3 3a x 例1. 思考: 设 (  为任意常数 ),  y  x 问 可得

例2. 设 y=eax, 求y(n)解: y'=aeax, y"=a’eax,y"y(n) =a"eax1- x特别有：(e")(n) =er1(1- x)例3. 设 y= ln(1+x),求 y(n)11·2y"= (-1)2解：(1 +x)2(1 +x)31+xj(n) = (-1)"-1 (n-1)!规定0！=1(1+x)n思考: =ln(1-x),y() =-(n-1)!(1-x)n

n (1 x) e , , y   a 3 ax  例2. 设 求 解: 特别有: 解: (n 1)! 规定 0 ! = 1 思考: e , ax y  . (n) y e , ax y   a e , 2 ax y   a n n ax y a e ( )  x n x (e ) e ( )  例3. 设 求 , 1 1 x y    , (1 ) 1 2 x y     , (1 ) 1 2 ( 1) 3 2 x y       (n) y 1 ( 1)   n x y     1 1 y    2 (1 ) 1  x 

例4. 设y= sinx,求y(n)解: y'=cosx =sin(x+)y"= cos(x+) = sin(x++)= sin(x + 2 · )J" = cos(x+2·)= sin(x +3·号一般地，(sinx)(n)=sin(x+ n·)类似可证：(cos x)(n) = cos(x+ n·)

例4. 设 求 解: y   cos x sin( ) 2 π  x  cos( ) 2 π y   x  sin( ) 2 π 2 π  x   sin( 2 ) 2 π  x   cos( 2 ) 2 π y   x   sin( 3 ) 2 π  x   一般地 , x  x  n (sin ) sin( ( ) 类似可证: x  x  n (cos ) cos( ( ) ) 2 π n  ) 2 π n 

二、高阶导数的运算法则设函数u=u(x）及v=v(x)都有n阶导数，则1. (u±v)(n) =u(n) ±v(n)2. (Cu)(n) = Cu(n）(C为常数)n(n-1)(n-23. (uv)(n) =u(n)v+ nu(n-l)y' +22!规律n(n -l)...(n - k +1)(n-k),(k)十·k!+..+uv(n)莱布尼茨（Leibniz）公式规律

规律 二、高阶导数的运算法则 都有 n 阶导数 , 则 (C为常数) 2! n(n 1) ! ( 1) ( 1) k n n  n  k      莱布尼茨(Leibniz) 公式 设函数 及 规律

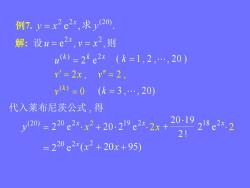
例7. = x2 e2x,求y(20)解：设u=e2x,= x2,则u(k) = 2ke2x (k =1,2,.*,20)v'=2x, v"=2,v(k) = 0 (k = 3,.., 20)代入莱布尼茨公式，得20.1918e2x.2y(20) = 220 e2x. x2 + 20 . 219 e2x. 2x2!=220e2x(x?+20x+95)

例7. 求 解: 设 e , , 2 2 u v x x   则 k k x u ( ) 2  2 e v   2x , v   2 , 0 ( )  k v 代入莱布尼茨公式 , 得  (20) y 20 2 x 2 e 2  x 19 2 x  2 0  2 e  2x 2 ! 2019   2 18 2 x 2 e ( k  1 , 2 ,  , 2 0 ) (k  3 ,  , 2 0)

内容小结高阶导数的求法（1）逐阶求导法(2）利用归纳法(3）间接法——利用已知的高阶导数公式如下列公式(sin x)(n) = sin(x + n ·)(cos x)(n) = cos(x + n ·)n!)(n) = (-1)n(a+ x)n+1十（4）利用莱布尼茨公式

内容小结 (1) 逐阶求导法 (2) 利用归纳法 (3) 间接法 —— 利用已知的高阶导数公式 (4) 利用莱布尼茨公式 高阶导数的求法     1 (n) a x 1 ( ) ! ( 1)    n n a x n 如下列公式 x  x  n (sin ) sin( ( ) x  x  n (cos ) cos( ( ) ) 2 π n  ) 2 π n 

作业P1001 (7) .(11), (12);3 (2);4 (2); 9 ; 10 (2)第四节

作业 P100 1 (7) ,(11), (12) ; 3 (2); 4 (2) ; 9 ; 10 (2) 第四节