《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-6极限存在准则 两个重要极限

第六节极限存在准则两个重要极限一、函数极限与数列极限的夹逼准则两个重要极限二D
二、 两个重要极限 一、函数极限与数列极限的夹逼准则 第六节 极限存在准则 两个重要极限

1.数列极限的夹逼准则(准则I)(l)yn≤xn≤zn(n=l,2,)limxn=a(2) lim yn = lim zn = αn→00n8n8证:由条件(2),V>0,3N,N2当n>N时,yn-aN,时,|znαN 时,有a-<yna+,a-<zn<a+,由条件(1)a-yn≤xn≤zn<a+即x,-a<,故limxn=a.n-0
y z a n n n n (2) lim lim 1. 数列极限的夹逼准则(准则I) (1) y x z ( n 1, 2 , ) n n n x a n n lim 证:由条件 (2) , 0 , , N1 当 时, 当 时, 令 max , , N N1 N2 则当 n N 时, 有 由条件 (1) n n n a y x z a 即 x a , n 故 lim x a . n n , N2

2.函数极限存在的夹逼准则(准则I')当xeU(xo,)时, g(x)≤f(x)≤ h(x),且(|x|>X >0)lim g(x) = lim h(x)= AX→XoX→X0(X0)(x→(00)lim f(x)= AX→Xo(0)
2. 函数极限存在的夹逼准则(准则Iʹ) ( , ) , 当 x U x0 时 g x h x A x x x x lim ( ) lim ( ) 0 0 g ( x) f (x) h( x) , f x A x x lim ( ) 0 ( x X 0 ) ( x ) ( x ) ( x ) 且

例1 求 limn-→00/n+nn解In2++In+nn1n又limlimn->00n-00Vn+nnnlimlim由夹逼准则得n→>8n20limn-00七Jn+n2
例1 2 2 2 1 1 1 lim ( ). 1 2 求 n n n n n 解 2 2 2 2 1 1 , 1 1 n n n n n n n n 2 1 lim lim 1 1 又 n n n n n n 1, 2 2 1 lim lim 1 1 1 n n n n n 1, 由夹逼准则得 2 2 2 1 1 1 lim( ) 1. 1 2 n n n n n

3.单调有界准则如果数列x满足条件单调增加X≤x..≤x≤xntI≤..,单调数列单调减少X ≥x2..≥xn ≥xn+1 ≥..",准则II单调有界数列必有极限几何解释:AMXXX2Xxnn+1
3.单调有界准则 如果数列xn 满足条件 1 2 1 , n n x x x x 单调增加 1 2 1 , n n x x x x 单调减少 单调数列 几何解释: x 1 x 2 x 3 x n x n 1 x A M 准则II 单调有界数列必有极限

例2证明数列x=V3+V3+...+V3(n重根式)的极限存在证显然x+1>x,:{x,}是单调递增的;又: x = V00A =3+A 解得 A= I+V4_1-V/13(舍去)221+/13..limx, =2n-00
例 2 3 3 3 ( ) . 证明数列 重 根 式 的 极 限 存 在 n x n 证 1 显 然 , n n x x 是 单 调 递 增 的 ; n x 1 又 x 3 3, 假 定 3, k x 1 3 k k x x 3 3 3, 是有界的 ; n x lim . n 存在 n x 1 3 , n n x x 2 1 3 , n n x x 2 1 lim lim(3 ), n n n n x x 2 A A 3 , 1 13 1 13 , 2 2 解 得 A A (舍去 ) 1 13 lim . 2 n n x

两个重要极限RAD二、1sinx1. lim=1Ax-0 x证:当xE(0,)时,△AOB的面积<圆扇形AOB的面积<AAOD的面积即1sinx<ix<1tanx故有(0<x<)sinxcOSxsinx(0<|x|<)显然有COSXXsinxlim下面再证明:limcosx=1.二-0X-0x
1 sin cos x x x 圆扇形AOB的面积 二、 两个重要极限 证: 当 即 sin x 2 1 tan x 2 1 亦即 sin tan (0 ) 2 π x x x x ( 0 , ) 2 π x 时, (0 ) 2 π 显然有 x △AOB 的面积< <△AOD的面积 故有 O B A x 1 D C
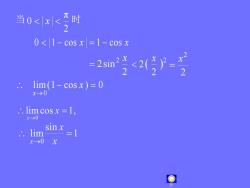
当0x时0<|1- cos x=1- cos x<2(=号= 2sin2×<lim(1- cosx)= 0x-0:.limcosx=1x-0sinxlimx-0x
注 当 2 π 0 x 时 0 1 cos x 1 cos x 2 2sin2 x 2 2 2 x 2 2 x lim(1 cos ) 0 0 x x

tanx例3.求limx0xtanxsinx解:limlim1x-0Xx-00xcOSxsinx= limlimx-0xx-0coSxarcsinx例4.求limx-0x解:令t=arcsinx,则x=sint,因此1原式=limlimsintt-osintt->0
例3. 求 解: x x x tan lim 0 x x x x cos sin 1 lim 0 x x x sin lim 0 x cos x 1 lim 0 1 例4. 求 解: 令 t arcsin x , 则 x sin t , 因此 原式 t t t sin lim 0 t sint 1

说明:一般地sin p(x)lim0(x)→0p(x)-COSX例5. 求 limx-0X2sinsin解:原式=limimx-012x0
2 0 sin lim x 2 x 2 x 2 1 例5. 求 解: 原式 = 2 2 2 0 2sin lim x x x 2 1 2 1 说明: 一般地
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-5 极限运算法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-4 无穷小与无穷大.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-3 函数极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-2 数列极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-1 映射与函数.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-10 闭区间上连续函数的性质.pdf
- 《高等数学》课程教学资源(书籍教材)同济大学高等数学第七版上册.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章_4.4有理函数的积分.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章_4.3分部积分.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章_4.2换元积分法.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章_4.1不定积分的定义和性质.pdf
- 《高等数学》课程教学资源(课件讲稿)第六章_6.3定积分在物理学上的应用.pdf
- 《高等数学》课程教学资源(课件讲稿)第六章_6.2定积分在几何上的应用.pdf
- 《高等数学》课程教学资源(课件讲稿)第六章_6.1定积分的元素法.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章_5.5反常积分的审敛法.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章_5.4反常积分.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章_5.3定积分的换元法和分部积分法.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章_5.2微积分基本公式.pdf
- 《高等数学》课程教学资源(课件讲稿)第五章_5.1定积分的概念和性质.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章_2.5函数的微分.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-7 无穷小比较.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-8 函数的连续性与间断点.pdf
- 《高等数学》课程教学资源(课件讲稿)第一章 函数与极限_1-9 连续函数的运算与初等函数的连续性.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-1 微分中值定理.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-2 洛必达法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-3 泰勒公式.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-4 函数的单调性与曲线的凸凹性.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-5 函数的极值与最大值最小值.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-6 函数图形的描绘.pdf
- 《高等数学》课程教学资源(课件讲稿)第三章 微分中值定理与导数的应用_3-7 曲率.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-1 导数概念.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-2 求导法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-3 高阶导数.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-4 隐函数和参数方程求导及相关变化率.pdf
- 《高等数学》课程教学资源(课件讲稿)第二章 导数与微分_2-5 函数的微分.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章 不定积分_4-2 换元积分法.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章 不定积分_4-3 分部积分法.pdf
- 《高等数学》课程教学资源(课件讲稿)第四章 不定积分_4-4 有理函数的积分.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-1 微分方程的基本概念.pdf
- 《高等数学》课程教学资源(课件讲稿)第七章 微分方程_7-2 可分离变量微分方程.pdf
