《高等数学》课程教学资源（课件讲稿）第三章 微分中值定理与导数的应用_3-5 函数的极值与最大值最小值

第五节第三章函数的极值与最大值最小值一、函数的极值及其求法二、最大值与最小值问题

二、最大值与最小值问题 一、函数的极值及其求法 第五节 函数的极值与 最大值最小值 第三章

一、函数的极值及其求法定义：设函数f(x)在(a,b)内有定义，xo E(a,b)若存在xo的一个邻域，在其中当x≠xo时，(1）f(x）f(xo），则称xo为f(x）的极小值点，称f（xo）为函数的极小值极大值点与极小值点统称为极值点

定义: 在其中当 时, (1) 则称 为 的极大值点 , 称 为函数的极大值 ; (2) 则称 为 的极小值点 , 称 为函数的极小值 . 极大值点与极小值点统称为极值点 . 一、函数的极值及其求法

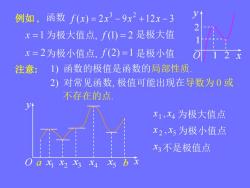
V例如，函数f(x)=2x3-9x2+12x-32x=1为极大值点，f(1)=2是极大值x=2为极小值点，f(2）=1是极小值O12注意：1）函数的极值是函数的局部性质2）对常见函数，极值可能出现在导数为0或不存在的点X1,X4为极大值点X2,X5为极小值点X3不是极值点Oaxxxxxbx

注意: 3 x x1 4 O a x b x y 1 4 x , x 为极大值点 2 5 x , x 为极小值点 3x 不是极值点 2) 对常见函数, 极值可能出现在导数为 0 或 不存在的点. 1) 函数的极值是函数的局部性质. ( ) 2 9 1 2 3 3 2 例如 , f x  x  x  x  为极大值点, 是极大值 为极小值点, 是极小值 函数 1 2 O x y 1 2 2 x 5 x

定理1（极值第一判别法）设函数f(x）在xo的某邻域内连续，且在空心邻域内有导数，当x由小到大通过xo时，(1)f(x）“左正右负”，则f(x)在xo取极大值(2)f(x）“左负右正”,则f(x)在xo取极小值；点击图中任意处动画播放暂停

定理 1 (极值第一判别法) ( ) , 设函数 f x 在 x0 的某邻域内连续 且在空心邻域 内有导数, , 当x由小到大通过 x0时 (1) f (x) “左正右负” , ( ) ; (2) f (x) “左负右正” , 则 f x 在 x0 取极小值 ( ) . 则 f x 在 x0 取极大值 点击图中任意处动画播放\暂停

例1.求函数f(x)=(x-1)x3 的极值解:1)求导数(a)=x3+(x-1)x-=量2）求极值可疑点令f(x)=0,得x=；令f()= 00,得x=03）列表判别|(0,3) 131(g,+8)(-8,0)01f'(x)-0.33f(x): x=0 是极大值点,其极大值为f(0)=0 —14x是极小值点，其极小值为f（）=-0.33X=

例1. 求函数 的极值 . 解: 1) 求导数   3  2 f (x) x 3 1 3 2 ( 1)  x   x 3 5 2 3 5 x x   2) 求极值可疑点 令 f ( x)  0 , 得 ; 5 2 x1  令 f ( x)   , 得 0 x2  3) 列表判别 x f (x) f (x)  0 5 2 0    0  0.33 ( , 0) (0 , ) 5 2 ( , ) 5 2   是极大值点，其极大值为 是极小值点，其极小值为 1 x y 1 O

定理2（极值第二判别法）设函数f(x）在点xo处具有二阶导数，且f'(xo)=0,f"(xo)≠0()若f"(xo）0,则f(x)在点xo取极小值I'(x)-I'(x0) = lim I(x)证:(1) f"(xo)= lim X→XOX-Xox→Xo X-Xof'(x)由f"(xo)0,当00;当xo<x<xo +时,f'(x)<0,XoSXo X+S由第一判别法知f(x）在xo取极大值(2）类似可证

定理2 (极值第二判别法) 二阶导数 , 且 则 在点 取极大值 ; 则 在点 取极小值 .   证: (1) ( ) 0 f  x 0 0 ( ) ( ) lim 0 x x f x f x x x       0 ( ) lim 0 x x f x x x     ( ) 0 , 由 f  x0  知 存在   0 , 0 , 当  x  x0   时 故 当 x0    x  x0时 ，f ( x)  0; 当x0  x  x0   时 ，f ( x)  0 , 0 x 0 x0   x    由第一判别法知 ( ) . f x 在 x0 取极大值 (2) 类似可证

例2.求函数 f(x)=(x2-1)3+1的极值解：1）求导数f'(x) = 6x(x2 -1)2, -f"(x)= 6(x2 - 1)(5x2 -1)2)求驻点令f(x)=0，得驻点 xj =-1,x2=0,X =13)判别因f"(0)=6>0，故f(0)=0为极小值；又f"(-1)=f"(1)=0,故需用第一判别法判别由于f(x)在x=±1左右邻域内不变号.f(x）在x=±1没有极值01 x

例2. 求函数 的极值 . 解: 1) 求导数 ( ) 6 ( 1) , 2 2 f  x  x x  ( ) 6 ( 1) (5 1) 2 2 f  x  x  x  2) 求驻点 令 f ( x)  0 , 得驻点 1, 0 , 1 x1   x2  x3  3) 判别 因 f (0)  6  0 , 故 为极小值 ; 又 f (1)  f (1)  0 , 故需用第一判别法判别. 1 x y 1 O

定理3(判别法的推广：拐点的判别法)设函数f(x)在点x处具有三阶导数，且f"（x）=0,f"（x）≠0()若f"(x）0,则f(x)的图形经过点xo由凸变凹所以(xo,f(xo)为拐点如： 对于y=x3,y' = 3x?, y" = 6x, y" = 6.1X且 y"x=o = 0, J" Ix=0=6>0.所以y=x的图形经过（0,0)时由凸变凹，(0,0)是一个拐点

定理3 (判别法的推广:拐点的判别法) 具有三阶导数 , 且 则 的图形经过点 由凹变凸; 则 的图形经过点 由凸变凹. 所以 0 0 ( , ( )) . x f x 为拐点 如： 对于 2 y x   3 , 且 1 x y 1 O

例如，例2中 f(x)=(x2-1)3+1f'(x) = 6x(x2 -1)2, f'(±l) = 0, f'(0) = 0-101xf"(x) = 6(x2 -1)(5x2 - 6), f"(±1)= 0f"(0)=36>0.=x=0是极小值点f"(x)= 24 x(5x2 - 3), f"(±1)± 0:(-1,1)和(1,1)是拐点说明：极值的判别法（定理1～定理3）都是充分的当这些充分条件不满足时，不等于极值或拐点不存在

例如 , 例2中 ( ) 2 4 (5 3), 2 f  x  x x  f (1)  0 说明: 极值的判别法( 定理1 ~ 定理3 ) 都是充分的. 当这些充分条件不满足时, 不等于极值或拐点不存在. 1 x y f x x x ( ) 6( 1)(5 6),    2 2 1 O 2 2 f x x x ( ) 6 ( 1) ,   f ( 1) 0,   f (0) 0.  f ( 1) 0,   f (0) 36 0.     x 0 . 是极小值点  ( 1,1) (1,1) . 和 是拐点

二、最大值与最小值问题若函数f(x)在闭区间[a,bl上连续，则其最值只能在极值点或端点处达到求函数最值的方法：(1）求f(x）在（a,b）内的极值可疑点Xi,X2,...,Xm(2）最大值M = max( f(x), f(x2),.*, f(xm), f(a), f(b))最小值m=min(f(x), f(x2), ., f(xm), f(a),f(b))

二、最大值与最小值问题 则其最值只能 在极值点或端点处达到 . 求函数最值的方法: (1) 求 在 内的极值可疑点 (2) 最大值 M  max f (a), f (b ) 最小值