《高等数学》课程教学资源（课件讲稿）第三章 微分中值定理与导数的应用_3-2 洛必达法则

1.设f(x）EC[0,元],且在（0,元)内可导，证明至少存在一点三E（O,元),使f'()=-f()cot2.证明：当e-（(b-a）3.设f(x)eC[a,b],且在(a,b)内可导,证明至少存在一点=E（a,b),使bf(b)- f(a)=Ef'()In?

1. 设 f (x)  C[ 0 , π ], 且在 ( 0, π ) 内可导, 证明至少存 在一点   ( 0 , π ), 使 f ( )   f ( ) cot . 2. 证明: 2 2 2 2 4 e e ln ln ( ). e 当       a b b a b a 时， 3. 设 f x C a b ( ) [ , ],  且在 ( , ) a b 内可导, 证明至少存 在一点   ( , ) , a b 使 ( ) ( ) ( ) ln . b f b f a f a    

第二节洛必达法则型未定式型未定式三、其他未定式

三、其他未定式 二、 型未定式 一、 型未定式 0 0 第二节 洛必达法则

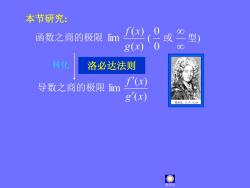
本节研究：0f(α)8或二型)函数之商的极限lim0g(x)8转化洛必达法则f(α)导数之商的极限limg'(x)格必达G-A.d洛必达

函数之商的极限 导数之商的极限 转化 ( 或 型) 本节研究: 洛必达法则 洛必达

本节研究：0f(x)8或二型)函数之商的极限lim0g(x)8转化洛必达法则f'(x)导数之商的极限limg'(x)1694年

函数之商的极限 导数之商的极限 转化 ( 或 型) 本节研究: 洛必达法则

福型未定式O定理 1.1) lim f(x)= lim F(x)= 0x-ax→a2)f(x)与F(x)在U(a)内可导,且F(x)±0f'(x)3) lim存在(或为）x→a F'(x)()= lim a)→ lim （洛必达法则）x→>aF(x)x-→aF'(x)

一、 ( ) ( ) 3) lim F x f x x a    存在 (或为 ) ( ) ( ) lim ( ) ( ) lim F x f x F x f x x a x a      2) f (x)与F (x) 在U (a)内可导,  定理 1. 型未定式 0 0 (洛必达法则)

f(x)= lim (a)lim洛必达法则x->a F(x) x->a F'(x)推论1.定理1中x→α换为下列过程之一：xaxax0,x+00,x-00条件2）作相应的修改，定理1仍然成立f'(x)0推论2.若lim仍属型，且f(x）,F(x）满足定F(x)0理1条件，则f(x)f'(x)f"(x)=limlimlim一F'(x)F"(x)F(x)定理1

推论1. 定理 1 中 x  a 换为下列过程之一: ,   x a 推论 2. 若 ( ) ( ) lim F x f x   理1条件, 则 条件 2) 作相应的修改 , 定理 1 仍然成立. x    , 洛必达法则 定理1

x3 -3x+20型例1.求1lim0x3 -x2 -x+1x3x2-3整lim解：原式x-1 3x2- 2x-136x洛三lim2x→16x-2注意：不是未定式不能用洛必达法则！6x0limlim 二=士x-→16x-2x→16

例1. 求 解: 原式 型 0 0 2 3  注意: 不是未定式不能用洛必达法则 ! 6 2 6 lim 1 x  x x 1 6 6 lim 1   x 3 3 2 x  3 2 1 2 x  x  lim 1  x 洛 6 2 6 lim 1    x x x 洛

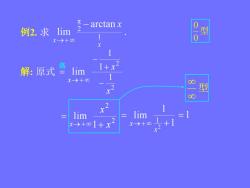
元-arctanx02型lim例2.求0X+8洛二解：原式lim→+008型8limlimX→+80→+01+x

例2. 求 解: 原式     x lim 型 0 0 2 2 1 lim x x x      1 2 1 1  x  2 1 x  1 1 lim 2 1     x x 型   洛

二型未定式二、8定理2.1) lim f(x)= lim F(x)= 00x→axa2）f(x)与F(x）在U(a)内可导,且F(x)±0f'(x)存在 (或为)3) limx-→>aF'(x)f(x)f'(x)= limlim（洛必达法则）x-aF(x)x-→>a F'(x)

二、   型未定式 ( ) ( ) 3) lim F x f x x a    存在 (或为∞) ( ) ( ) lim F x f x xa 定理 2. ( ) ( ) lim F x f x x a     (洛必达法则) 2) f (x)与F (x) 在U (a)内可导, 

说明：定理中x→α换为x→atx→aX-X→+8,X--00之一，条件2）作相应的修改，定理仍然成立定理2

说明: 定理中 x  a 换为 之一, 条件 2) 作相应的修改 , 定理仍然成立. ,   x a ,   x a x   , x    , x    定理2