《高等数学》课程教学资源（课件讲稿）第四章 不定积分_4-3 分部积分法

第三节第四章分部积分法由导数公式(uv)'= u'v+uv积分得：uv = [u'vdx + [ u'dx[u'dx=uv- [u'vdx分部积分公式或「udv=uv-Jvdu选取u及（或dv）的原则：1)v容易求得；2)[u'vdx比[uv'dx容易计算

第三节 由导数公式 (uv)  u  v  uv  积分得: uv  u  vdx  uv dx   分部积分公式 uv dx uv u v dx       或 ud v uv v d u     1) v 容易求得 ; 容易计算 . 分部积分法 第四章

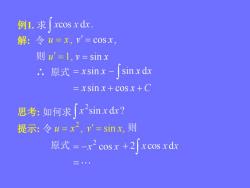
xcos x dx.例1.求解：令u=x，v=cosx,则u'=l,v=sinxsinx dx: 原式 =xsinx-=xsinx+cosx+Cxsinxdx?思考：如何求提示：令u=x2，'= sin x,则原式 =-x2 cosx +2[xcos xdx

例1. 求 解: 令 u  x , v   cos x , 则 u   1, v  sin x ∴ 原式  x sin x   sin x dx  x sin x  cos x  C 思考: 如何求 提示: 令 , 2 u  x v   sin x, 则 原式

例2.求[xln xdx.解：令u=lnx，=x则原式：xdx

例2. 求 x ln x dx.  解: 令 u  ln x , v   x 则 , 1 x u   2 2 1 v  x 原式 = x ln x 2 1 2   x dx 2 1  x x  x  C 2 2 4 1 ln 2 1

x arctan x dx例3.求解：令u=arctanx,v'= x则·原式arctanx1福dxarctan x21-x-arctan x)+CarctanxC

例3. 求 x arctan x dx.  解: 令 u  arctan x , v   x 则 , 1 1 2 x u    2 2 1 v  x ∴ 原式 x arctan x 2 1 2     x x x d 2 1 1 2 2 x arctan x 2 1 2      x x ) d 1 1 (1 2 1 2 x arctan x 2 1 2   (x  arctan x)  C 2 1

例4.求「esinxdx解：令u=sinx,v'=ex，则u'= cosx, v=er原式=e*sinx-[ecosxdx再令u=cosx,v=e*则u'=-sinx, v=ex=e"sin x -e"cos x-[e"sinx dx故原式= e*(sinx-cosx)+C说明：也可设u=ev为三角函数，但两次所设类型必须一致

例4. 求 e sin x dx. x  解: 令 u  sin x , x v   e , 则 u   cos x , x v  e ∴ 原式 x x  e sin   x x x e cos d 再令 u  cos x , x v   e , 则 u   sin x , x v  e x x  e sin   x  x x x x e cos e sin d 故 原式 = x x C x e (sin  cos )  2 1 说明: 也可设 为三角函数 , 但两次所设类型 必须一致

解题技巧：选取u及V的一般方法：把被积函数视为两个函数之积，按“反对幂指三”的反：反三角函数顺序，前者为u后者为v'对：对数函数例5.求|arccos x dx.幂：幂函数指：指数函数解：令u=arccosx,=l则三：三角函数V=xdx原式=xarccosx= x arccos x -2[(1-x2)d(1 -x2)= x arccos x- ~1 - x2 +C

解题技巧: 把被积函数视为两个函数之积 , 按 “ 反对幂指三” 的 顺序, 前者为 u 后者为 v  . 例5. 求 解: 令 u  arccos x , v   1 , 则 , 2 1 1 x u     v  x 原式 = x arccos x    x x x d 2 1  x arccos x (1 ) d(1 ) 2 2 2 1 2 1      x x  x arccos x  x  C 2 1 反: 反三角函数 对: 对数函数 幂: 幂函数 指: 指数函数 三: 三角函数

lncosx例6.求dxcos?x.则解：令u=lncosxvcosxu'=-tanx, v=tanx[tan?x dx原式=tanx·lncosx+= tan x Incos x + [(sec2? x -1)dx= tanx·lncosx +tanx- x+C

例6. 求 解 : 令 u  ln cos x , x v 2 cos1   , 则 u   tan x , v  tan x 原式 = tan x ln cos x   tan x dx 2  tan x ln cos x   (sec x 1) dx 2  tan x ln cos x  tan x  x  C

例7. 求[evx dx.解：令/x=t,则x=t2,dx=2tdt原式=2[te'dtI 令u=t,v'=e'=2(te'-fe'dt)= 2(te'-e') +C= 2e/x(Vx -1)+C

例7. 求 解: 令 x  t , 则 , 2 x  t dx  2t d t 原式 t t t 2 e d    t  2 t e x C x  2e ( 1)  u  t , t v   e e ) t   C 令 t  2(t e t  t e d  

例8.设 I,=「sin"xdx(nEN)，证明递推公式:n-1In = --sin"-lIn-2 (n≥2)+xcoSx+nn证：= [ sin"-x · sin xdx =-{ sin"-xd(cos x)= -sin"-I x cos x + [cosxd( sin"-l x)= -sinn-I xcos x +[ cosx ·(n -1)sin"-2 xcos xdx= -sin"- xcos x+(n -1)[ cos’ xsin"-2 xdx= -sin"-l xcosx +(n-1)[(1-sin2 x)sin"-2 xdx= -sin"-I xcos x +(n-1)[ sinn-2 xdx -(n-1)[ sin" xdxn-lIn-2 (n≥2)--sin"n-l-xcoSx+nn

例8. 设 证: 证明递推公式: 1 2 1 1 sin cos ( 2) n n n n I x x I n n n        1 sinn n I x     sin dx x 1 sin d(cos ) n x x    1 1 sin cos cos d(sin ) n n x x x x       1 sin cos n x x    2 cos ( 1)sin cos d n x n x x x      1 sin cos n x x    2 2 ( 1) cos sin d n n x x x     1 sin cos n x x    2 2 ( 1) (1 sin )sin d n n x x x      1 sin cos n x x    2 ( 1) sin d ( 1) sin d n n n x x n x x        1 2 1 1 sin cos ( 2) n n n n I x x I n n n        

说明：分部积分题目的类型1）直接分部化简积分：2）分部产生循环式，由此解出积分式：（注意：两次分部选择的u，V函数类型不变例4解出积分后加C）3）对含自然数n的积分，通过分部积分建立递推公式

说明: 分部积分题目的类型: 1) 直接分部化简积分 ; 2) 分部产生循环式 , 由此解出积分式 ; (注意: 两次分部选择的 u , v 函数类型不变 , 解出积分后加 C ) 例4 3) 对含自然数 n 的积分, 通过分部积分建立递 推公式 . 例4