《高等数学》课程教学资源（课件讲稿）第三章课件_第三章第五节

第三章第五节函数的凹凸性函数作图曲线的凹凸与拐点一、曲线的渐近线二、三、函数作图HIGH EDUCATION PRESS机动目录上页下页返回结束

第五节 二、曲线的渐近线 机动 目录 上页 下页 返回 结束 一、曲线的凹凸与拐点 函数的凹凸性 函数作图 第三章 三、函数作图

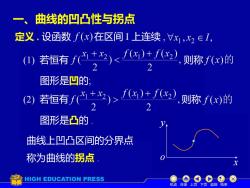
曲线的凹凸性与拐点一、定义.设函数 f(x)在区间I上连续,Vxi,x2 If(x)+ f(x2)X2则称f(x)的若恒有f1)22图形是凹的：f(x)+ f(x2)入则称f(x)的若恒有f((2)22图形是凸的曲线上凹凸区间的分界点称为曲线的拐点xHIGH EDUCATION PRESS机动目录上页下页返回结束

A B 定义 . 设函数 在区间 I 上连续 , (1) 若恒有 则称 图形是凹的; (2) 若恒有 则称 曲线上凹凸区间的分界点 称为曲线的拐点 . 图形是凸的 . y o x1 x2 x 2 1 2 x +x y o x1 x 2 1 2 x +x 2 x y o x 一、曲线的凹凸性与拐点 机动 目录 上页 下页 返回 结束

定理2.设函数f(x)在区间I上有二阶导数(1)在I内f"(x)>0,则f(x)在I内图形是凹的(2)在 I内,f"(x)<0,则f(x)在I内图形是凸的确定曲线y=x的凹凸性和拐点确定曲线y=x的凹凸性和拐点确定曲线=x4的凹凸性和拐点HIGH EDUCATION PRESS机动目录上页下页返回结束

定理2. (1) 在 I 内 则 在 I 内图形是凹的 ; (2) 在 I 内 则 在 I 内图形是凸的 . + − 机动 目录 上页 下页 返回 结束 设函数 在区间I 上有二阶导数 确定曲线 y = x 4 的凹凸性和拐点 确定曲线 的凹凸性和拐点 确定曲线 y x = 3 的凹凸性和拐点

凹凸区间及拐点的求法（1明确函数的定义域求出二阶导数等于零的点，及二阶不可导点(2在每个子区间上判断二阶导数的符号，判定曲线的凹凸性3)曲线上凹凸性发生变化的点即为拐点HIGH EDUCATION PRESS

凹凸区间及拐点的求法 (1)明确函数的定义域, 求出二阶导数等于零的点，及二阶不可导点 (2)在每个子区间上判断二阶导数的符号， 判定曲线的凹凸性 (3)曲线上凹凸性发生变化的点即为拐点

例.求曲线y=3x4－4x2+1的凹凸区间及拐点解: 1) y'=12x3 _12x2y" = 36x2 - 24x = 36x(x -3)2)令 y"=0(0.) (,)得X1=0,X2=3x023对应 =1,2=1(,+8)(0, 0(-8,0)X3) 判断0十02凹凹2Ly故该曲线在（-0,0)及(,+)上向上凹,在(0,)上(,2)均为拐点向上凸，点（0，1）及HIGH EDUCATION PRESS机动目录上页下页返回结束

36 ( ) 3 2 = x x − 例. 求曲线 的凹凸区间及拐点. 解: 1) 12 12 , 3 2 y  = x − x 2) 令 y  = 0 得 0 , , 3 2 x1 = x2 = 对应 3) 判断 27 11 1 2 y =1, y = (−,0) (0, ) 3 2 ( , ) 3 2 +  y  x y 0 3 2 + 0 0 1 27 11 − + 故该曲线在 (−,0) ( , ) 3 及 2 +  上向上凹, 向上凸 , 点 ( 0 , 1 ) 及 ( , ) 27 11 3 2 均为拐点. 在(0, 3 2 )上 凹 凸 凹 机动 目录 上页 下页 返回 结束 3 2 (0,1) ( , ) 27 11 3 2

、曲线的渐近线1、水平渐近线lim f(x)= Ax-8直线=A为曲线=f(x)的水平渐近线2、铅直渐近线lim f(x)= 00,x-→xo直线 x=xo为曲线=f(x)的铅直渐近线HIGH EDUCATION PRESS

f x A x = → lim ( ) 直线 y = A 为曲线 的水平渐近线 二、曲线的渐近线 1、水平渐近线 2、铅直渐近线 直线 0 x =x 为曲线 的铅直渐近线

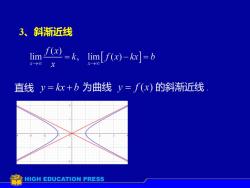
3、斜渐近线f(x)lim=k.lim[f(x)-kx] = bX-00x8x直线 =kx+b 为曲线 =f(x)的斜渐近线HIGHEDUCATION PRESS

3、斜渐近线 直线 为曲线 的斜渐近线

y = x + arctan x求该函数的斜渐近线口AFigure1X编辑(E)文件（F)查看V)插入（0）工具T桌面（D)窗口(W)帮助(H)-月日雪Q货00y1=x+atan(x)y2=x+pi/26y3=x-pi/2420-2-46-8-3-20123A5-4-15HIGHEDUCATION PRESS

求该函数的斜渐近线

三、函数作图步骤：1. 确定函数 y=f(x)的定义域,并考察其奇偶性及周期性;2. 求f'(x)，,f"(x),并求出f'(x)及f"(x)为 0 和不存在的点;3.列表判别增减及凹凸区间，求出极值和拐点：4. 求水平、铅直渐近线5.确定某些特殊点，描绘函数图形HIGHEDUCATIONPRESS机动目录上页下页返回结束

三、函数作图 步骤 : 1. 确定函数 的定义域 , 期性 ; 2. 求 并求出 及 3. 列表判别增减及凹凸区间 , 求出极值和拐点 ; 4. 求水平、铅直渐近线 ; 5. 确定某些特殊点 , 描绘函数图形 . 为 0 和不存在 的点 ; 并考察其奇偶性及周 机动 目录 上页 下页 返回 结束

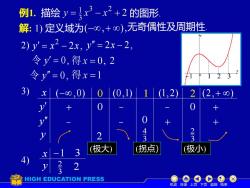
例1.描绘=↓x3-x2+2的图形解：1)定义域为(-00,+o0),无奇偶性及周期性2) y'= x2- 2x, y"= 2x-2令y=0,得x=0,2令y"=0,得x=13)x(-8,0) 02/(2,+8)1(0.1)/11(1.2)004323V2(拐点)(极大)(极小)3一X2V13HIGH EDUCATION PRESS机动目录上页下页返回结束

例1. 描绘 的图形. 解: 1) 定义域为 无奇偶性及周期性. 2) 2 , 2 y  = x − x y  = 2x − 2, 令 y  = 0, 令 y  = 0, 3) x y  y  y (− ,0) 0 (0,1) 1 (1,2) 2 (2,+ ) + 0 − − 0 + − − + + 2 3 4 (极大) (拐点） 3 2 (极小) 4) x y −1 3 3 2 2 0 机动 目录 上页 下页 返回 结束 −1 1 2 3