《高等数学》课程教学资源（PPT课件）第八章向量代数与空间解析几何_第六节空间曲线及其方程

第六节空间曲线及其方程、空间曲线的一般方程一二、空间曲线的参数方程N三、空间曲线在坐标面上的投影返回MathGS公式上页下页线与面数学家

第六节 空间曲线及其方程 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影

第六节空间曲线及其方程一、空间曲线的一般方程设曲面Su，S,的方程分别为S, : F(x,y,z) = 0,SS2 : G(x, y,z) = 0 ,则它们的交线方程为7F(x,y,z)=0,G(x, y,z)= 0,S称之为空间曲线的一般方程MathGS公式下页返回线与面数学家上页

第六节 空间曲线及其方程 一、空间曲线的一般方程 设曲面S1，S2的方程分别为 x y z S1 S2 则它们的交线方程为 称之为空间曲线的一般方程

第六节空间曲线及其方程x? +y? =1,例1 方程组表示怎样的曲线？2x+3v+3z =61返回MathGS公式数学家上页下页线与面

第六节 空间曲线及其方程 例1 方程组    + + = + = 2 3 3 6 1, 2 2 x y z x y 表示怎样的曲线？ x y z x y z

第六节空间曲线及其方程x2+y?+z2= 4例2方程组表示怎样的曲线？(x-1)? +y? =17返回MathGS公式数学家上页下页线与面

第六节 空间曲线及其方程 例2 方程组    − + = + + = ( 1) 1 4 , 2 2 2 2 2 x y x y z 表示怎样的曲线？ x y z x y z z x y

第六节空间曲线及其方程二、空间曲线的参数方程将曲线C上的动点坐标x,yz表示成参数t的函数：x = x(t),y= y(t),(z = z(t),称它为空间曲线的参数方程返回MathGS公式上页下页线与面数学家

第六节 空间曲线及其方程 二、空间曲线的参数方程 将曲线C上的动点坐标 x, y, z表示成参数 t 的函数: 称它为空间曲线的参数方程

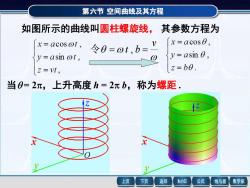
第六节空间曲线及其方程如图所示的曲线叫圆柱螺旋线，其参数方程为x=acos0x=acosot,令0=のt,b:y=asin 0,y=asin ot,z=bo.z =vt,当0=2元，上升高度h=2元b，称为螺距返回MathGS公式上页下页线与面数学家

第六节 空间曲线及其方程 x y z 如图所示的曲线叫圆柱螺旋线，    v 令 = t , b = 当 = 2，上升高度 h = 2 b，称为螺距 . 其参数方程为 x y z O

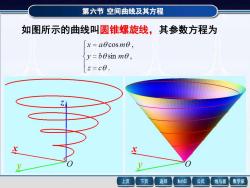
第六节空间曲线及其方程如图所示的曲线叫圆锥螺旋线，其参数方程为x=aocosmo,y=bosin mo,z=c0.XVVMathGS上页下页返回公式数学家线与面

第六节 空间曲线及其方程 如图所示的曲线叫圆锥螺旋线，其参数方程为 x y z O x y O

第六节空间曲线及其方程如图所示的曲线叫抛物螺旋线，其参数方程为x=acosme,y=bosin me,z =c0?7XLVMathGS数学家上页下页返回公式线与面

第六节 空间曲线及其方程 如图所示的曲线叫抛物螺旋线，其参数方程为 x y x y z O

第六节空间曲线及其方程例3将下列曲线化为参数方程,并在MathGS中画图x?+y? =1,x?+y?+z? =4,(1)(2)(x-1)? +y? =1.2x +3y+3z =6;x =1+cos0x = cos0y= sin 0(0≤0≤4元)y=sin0，(0≤0≤2元)IZ02Z = 2-z = 2sin-cosO-sin 237.VXx返回MathGS公式上页下页线与面数学家

第六节 空间曲线及其方程 x y z O 例3 将下列曲线化为参数方程,并在MathGS中画图.    − + = + + =    + + = + = ( 1) 1. 4 , (2) 2 3 3 6; 1, (1) 2 2 2 2 2 2 2 x y x y z x y z x y . cos sin , 3 2 2 sin , (0 2π) cos ,        = − − =   =      z y x (0 4π). , 2 2sin sin , 1 cos ,          = = = +     z y x x y z O

第六节空间曲线及其方程x=p(t),例4求空间曲线：y=(t)，(α≤t≤β),绕z轴旋z = の(t),转时的旋转曲面方程解 任取点 M,(p(t),y(t),w(t) e T, 点 M,绕z轴旋转转过角度后到点M(x,J,z)，则MZ(x=Vp (t)+y(t) cos , 16（(α≤t≤βIMy=/p(t)+y(t) sin 0, (0≤0≤2元z = w(t),这就是旋转曲面满足的参数方程下页返回MathGS公式数学家上页线与面

第六节 空间曲线及其方程 M M1  y z x O 绕 z 轴旋 转时的旋转曲面方程 . 解 点 M1绕 z 轴旋转, 转过角度 后到点 则 这就是旋转曲面满足的参数方程 . 例4 求空间曲线 任取点