《高等数学》课程教学资源（PPT课件）第十二章无穷级数_第七节傅里叶级数

第七节傅里叶级数一、引入基本概念函数展开成傅里叶级数一四、正弦级数和余弦级数返回MathGS公式上页下页线与面数学家

第七节 傅里叶级数 二、基本概念 四、正弦级数和余弦级数 三、函数展开成傅里叶级数 一、引入

第七节傅里叶级数一、引入在第四节中，我们讨论了将函数展开成幂级数的问题，在本节中，我们将讨论周期函数展开成三角级数的问题，正弦函数是一种常见而又简单的周期函数．例如描述简谐振动的函数振幅初相角频率y= Asin(の t +@)2元就是一个以为周期的正弦函数0下页返回MathGS公式数学家上页线与面

第七节 傅里叶级数 一、引入 在第四节中，我们讨论了将函数展开成幂级数的问 题，在本节中，我们将讨论周期函数展开成三角级数的 问题． 正弦函数是一种常见而又简单的周期函数．例如描 述简谐振动的函数 y = Asin( t +) 就是一个以  2π 为周期的正弦函数． 振幅 角频率 初相

第七节傅里叶级数那么其他非正弦函数的周期函数能否由不同频率的正弦函数叠加而成呢？请看下面的例子8sin nx>利用工具箱中的无例1设有函数项级数nn=l穷级数工具，研究(1)部分和Sk(x)是不是周期函数；(2)部分和Sk(x)的连续性：(3）部分和数列s(x)是否收敛MathGS上页下页返回公式线与面数学家

第七节 傅里叶级数 那么其他非正弦函数的周期函数能否由不同频率的 正弦函数叠加而成呢？ 请看下面的例子. 例1 设有函数项级数 , sin 1   n= n nx 利用工具箱中的无 穷级数工具，研究 (1) 部分和 sk (x) 是不是周期函数； (2) 部分和 sk (x) 的连续性； (3) 部分和数列 sk (x) 是否收敛

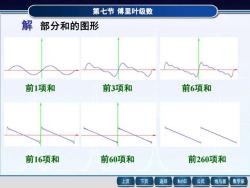
第七节傅里叶级数解部分和的图形前1项和前3项和前6项和前16项和前60项和前260项和返回MathGS公式上页下页线与面数学家

第七节 傅里叶级数 解 部分和的图形 前1项和 前3项和 前6项和 前16项和 前60项和 前260项和

第七节傅里叶级数由此可知(1)部分和Sk(x)是周期为2元的周期函数;(2)部分和 sk(x)在2k元(k=0,±1,±2,...)处不连续，在其他点处连续；(3)部分和数列 sk(x)收敛例1中的这些问题需要进行理论研究，这也是本节将要讨论的问题上页下页返回MathGS公式线与面数学家

第七节 傅里叶级数 由此可知 (1) 部分和 sk (x) 是周期为2 的周期函数； (2) 部分和 sk (x) 在2k (k=0,1, 2,.)处不连续，在 (3) 部分和数列 sk (x) 收敛. 其他点处连续； 例1中的这些问题需要进行理论研究，这也是本节 将要讨论的问题

第七节傅里叶级数二、 基本概念1.三角级数定义形如% + E(a, cos nx + b, sin nx)2n=1的级数叫做三角级数。例如引例中的函数项级数8sin nxZ就是三角级数nn=l返回MathGS公式上页下页线与面数学家

第七节 傅里叶级数 二、基本概念 定义 形如 ( cos sin ) 2 1 0 a nx b nx a n n + n +  = 的级数叫做三角级数 . 1. 三角级数 例如引例中的函数项级数   =1 sin n n nx 就是三角级数

第七节傅里叶级数2.三角函数系定义集合(1, cos x,sin x, cos2x,sin 2x,..., cosnx,sin nx,...在三角函数系中，任意两个不同的叫做三角函数系函数的乘积在区间「-元，元】上的积分等于零，任意两个相同函数的乘积在区间1-元，元上的积分不等于零，称即有三角函数系在区间[-元，元】上正交。返回MathGS公式上页下页数学家线与面

第七节 傅里叶级数 定义 集合 {1,cos x,sin x,cos 2x,sin 2x,  ,cos nx,sin nx, } 叫做三角函数系. 2. 三角函数系 在三角函数系中，任意两个不同的 函数的乘积在区间 [- , ] 上的积分等于零，任意两个 相同函数的乘积在区间 [- , ] 上的积分不等于零，称 三角函数系在区间 [- , ] 上正交. 即有

第七节傅里叶级数C元cosnx dx =0 (n=1,2,3, ..)元元sin nx dx =0 (n=1,2,3,..)元sin kxcosnx dx = 0 (k,n = 1,2,3, ..)元元coskxcosnx dx =0 (k,n=1,2,3,...,k±n)T元元sin kxsin nx dx =0 (k,n=1,2,3, ...,k ±n)元12dx=2元，T元元sin nx dx = 元cos~nxdx=元(n = 1,2,3, .)元元返回MathGS公式数学家上页下页线与面

第七节 傅里叶级数 cos d 0 ( 1,2,3, ), π π  = =  − nx x n sin d 0 ( 1,2,3, ), π π  = =  − nx x n sin cos d 0 ( , 1,2,3, ), π π  = =  − k x nx x k n cos cos d 0 ( , 1,2,3, , ), π π k x nx x = k n = k  n −  sin sin d 0 ( , 1,2,3, , ), π π k x nx x = k n = k  n −  1 d 2π , π π 2 = − x sin d π , cos d π ( 1,2,3, ). π π 2 π π  2 =  = =  − − nx x nx x n

第七节傅里叶级数三、函数展开成傅里叶级数设f(x)是周期为2元的周期函数，且能展开成三角级数：f(x) = % + (an cos nx + b, sin nx)21n=l下面来求系数ao,a1,b1，.….为此进一步假设上式右端的级数可逐项积分返回MathGS公式上页下页线与面数学家

第七节 傅里叶级数 三、函数展开成傅里叶级数 设 f (x) 是周期为 2 的周期函数，且能展开成三角 级数： ( cos sin ). 2 ( ) 1 0 a nx b nx a f x n n = + n +  = 下面来求系数 a0 , a1 , b1 , . . 为此进一步假设上式右端的级数可逐项积分

第七节傅里叶级数8f(x)=号+Z(a, cos n +b, sin x).n=先求αo两边从-元到元积分，得8αZ(a " cos kx dx+bk ]一dx + f(x) dx =sin kx dx)一元 2元k=1由三角函数系的正交性ao=二 " f(x) dx.元J下页返回MathGS公式数学家上页线与面

第七节 傅里叶级数 ( cos sin ). 2 ( ) 1 0 a nx b nx a f x n n = + n +  = 先求 a0 . 两边从 - 到  积分，得 d ( cos d sin d ). 2 ( ) d π π π π 1 π π 0 π π x a k x x b k x x a f x x k k    k − −  = − − = + + 由三角函数系的正交性 ( ) d . π 1 π π 0 a f x x − =