《高等数学》课程教学资源（PPT课件）第十一章 曲线积分与曲面积分_D11_4对面积的曲面积分

第十一章第四节对面积的曲面积分一、对面积的曲面积分的概念二、>对面积的曲面积分的计算法HIGHEDUCATION PRESS返回结束机动自录上页下页

第四节 一、对面积的曲面积分的概念 二、对面积的曲面积分的计算法 机动 目录 上页 下页 返回 结束 对面积的曲面积分 第十一章

对面积的曲面积分的概念一、引例设曲面形构件具有连续面密度x,y,z),求质量M.(5i,ni,S)，采用类似求平面薄板质量的思想，“分割，近似表示，求和，取极限的方法,可得ZM =limZp(5ini,S)As>01=1其中，入表示n小块曲面的直径的最大值（曲面的直径为其上任意两点间距离的最大者）HIGHEDUCATIONPRESS上页下页返回结束机动目录

o x y z 一、对面积的曲面积分的概念 引例: 设曲面形构件具有连续面密度 类似求平面薄板质量的思想, 采用 可得 M = 求质 “分割，近似表示，求和，取极限” 的方法,  量 M. 其中,  表示 n 小块曲面的直径的 最大值 (曲面的直径为其上任意两点间距离的最大者). 机动 目录 上页 下页 返回 结束

定义：设为光滑曲面，f(x,y,z)是在上有界，任意分割Z为 n小块AS,i=l,2,..…,n，在△S,上任意取点（si,ni,S），作乘积f（5i,niS)△S，n并作和Z（,,n,5)△S，，若→0时，此和式极限i=1存在，则称此极限为f(x,,2）在曲面上对面积的曲面积分或第一类曲面积分。 f(x, y,z)dS记作被积函数积分曲面HIGHEDUCATIONPRESS

定义: 设  为光滑曲面, 任意取点 ，作乘积 ， 曲面积分或第一类曲面积分。   f (x, y,z)d S f (x, y, z) 是在  上有界， 任意分割  为 n 小块， ，在 上 存在，则称此极限为 f (x, y, z) 在曲面  上对面积的 并作和 ，若 时，此和式极限 记作

nZlim[J f(x, y,z)dsf(si,ni,S)As10i=1D注:1.若函数f(x,y,2)在光滑曲面上连续，则一定可积曲面形构件的质量：M =I/ p(x,J,z)dS23.关于积分曲面的可加性: Ff(x, y,2)ds4.沿封闭曲面的积分面积元素：dS=/1+z+z,dxdy曲面Z面积：A=「ds6.HIGHEDUCATION PRESS

2. 曲面形构件的质量： 5. 面积元素： 注： 1. 若函数f (x, y, z) 在光滑曲面  上连续，则一定可积。 3. 关于积分曲面的可加性 4. 沿封闭曲面的积分： 6. 曲面  面积：

对面积的曲面积分的计算法----化为二重积分二、Z :z = z(x, y), (x,y) e Dxy定理：设有光滑曲面z(x,y)在D上具有一阶连续偏导数，f(x,y, z)在上连续，则曲面积分[ f(x,y,z)dsxy[[ J[x, y,z(x, y)l /1+ z + z, dxdyDHHIGH EDUCATION PRESS

o x y z 定理: 设有光滑曲面 f (x, y, z) 在  上 二、对面积的曲面积分的计算法- Dxy  连续，则曲面积分

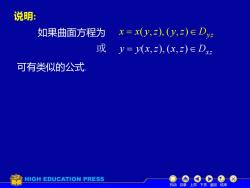
说明：x = x(y,z),(y,z)e Dy如果曲面方程为或y= y(x,z), (x,z)e Dx可有类似的公式HIGH EDUCATION PRESS机动目录上页下页返回结束

说明: Dyz x = x( y,z), ( y,z) Dxz 或 y = y(x,z), (x,z) 可有类似的公式. 如果曲面方程为 机动 目录 上页 下页 返回 结束

2++z=0例1计算曲面积分其中是球面 z=h(0<h<a)被平面截出的顶部。解：Z:z2 - h2 ,(z = 0)adxdypdp0+de+h福2元a2元alnHIGH EDUCATION PRESS目录上页返回结束机动下页

Dxy 例1 计算曲面积分 ,其中是球面 被平面 截出的顶部。 解: 2 2 2 2 Dxy : x + y  a − h 2 2 1 x y + z + z o x z y  h a 机动 目录 上页 下页 返回 结束

Fxyzds例2 计算其中是由平面x+y+z=l 与2坐标面所围成的四面体的整个边界曲面解: 设 Z1, 2,Z3,Z4 分别表示Z在平面x=0,y=0,z=0,x+y+z=1 上的部分1y在Z,,Z,,上被积函数xyz为零xyzds,故积分为0，只需计算xyzdS =xxy(l-x-y)/3dxd yxyzdS=DxyV3xdxy(1-x-y)dy =120HIGHEDUCATION PRESS

例2 计算 其中 是由平面 与 坐标面所围成的四面体的整个边界曲面。 o z y x 1 1 1 解: 设 上的部分, 1 2 3 4  ,  ,  ,   − − − x y x y y 1 0 (1 ) d  = 1 0 3 x dx 分别表示 在平面 故积分为0，只需计算

例3(x? +y?求抛物面壳（0≤z≤1）的质量ZE其面密度为p=z。/1+z+z =V≤2 (z=0)+x+y解:D:x2+y2[zdS = ,(x +y°)/1+x +y’dxdyM=dep?/1+p'dpp/1+ppdp/1+p2元(6/3 +1)兴(t2 -1)2t'dt 15HIGH EDUCATION PRESS

例3 解：

内容小结nY1. 定义：[[ f(x, y,z)dS = limf(Ei,ni,S)△S1-0Zi=12. 计算：设Z:z=z(x,y),(x,y)e Dxy,则[ f(x, y,z)dS= [[ f[x, y,z(x, y)]/1+z, + z,dxdyZDHIGH EDUCATION PRESS

内容小结 1. 定义 : i i i Si  f ( , , ) =ni 1 0 lim→ =  2. 计算: 设 : ( , ),( , ) , Dxy  z = z x y x y  则