《高等数学》课程教学资源（PPT课件）第十章 重积分_D10_1二重积分概念

第十章重积分一元函数积分学：定积分重积分曲线积分多元函数积分学曲面积分

第十章 一元函数积分学：定积分 多元函数积分学 重积分 曲线积分 曲面积分 重 积 分

第十章第一节二重积分的概念与性质一、 引例二、二重积分的概念三、 二重积分的性质HIGHEDUCATION PRESS返回结束机动自录上页下页

三、二重积分的性质 第一节 一、引例 二、二重积分的概念 机动 目录 上页 下页 返回 结束 二重积分的概念与性质 第十章

一、引例z= f(x,y)1.曲顶柱体的体积给定曲顶柱体底：xoy面上的闭区域DD顶：连续曲面 z=f(x,y)≥0侧面：以D的边界为准线，母线平行于z轴的柱面体积=？解法：类似定积分解决问题的思想“分割、近似代替、求和、取极限HIGH EDUCATION PRESS返回机动自录上页下页结束

解法: 类似定积分解决问题的思想: 一、引例 给定曲顶柱体: 底： xoy 面上的闭区域 D 顶: 连续曲面 侧面：以 D 的边界为准线 , 母线平行于 z 轴的柱面 体积=？ “分割、近似代替、求和、取极限” D 机动 目录 上页 下页 返回 结束

1)"分割"z= f(x,y)用任意曲线网分D为n个区域A01, A02, *"", Aon以它们为底把曲顶柱体分为 n个 f(s,n)小曲顶柱体D(5,n.)2)“近似代替Do在每个△o,中任取一点（si,n）则AV, ~ f(5i,ni)△o, i=1,2,.",n3)“求和”福AVf(si,n)Ai-lHIGH EDUCATION PRESS上页下页返回结束机动自录

D 1)“分割” 用任意曲线网分D为 n 个区域    n , , , 1 2  以它们为底把曲顶柱体分为 n 个 2)“近似代替” 在每个 3)“求和” 中任取一点 则 小曲顶柱体 机动 目录 上页 下页 返回 结束

4)“取极限z= f(x,y)定义的直径为f(S,n.)2(△o,) = max (/ PP2 I/ P,P, = △0;D(5,n.)Da记1(A0)3a=maxl1→0=1HIGH EDUCATION PRESS机动目录上页下页返回结束

4)“取极限” 记 机动 目录 上页 下页 返回 结束

2.平面薄片的质量有一个平面薄片，在xoy平面上占有区域D，其面密度为μ(x,y)EC,计算该薄片的质量 M若μ(x,)=μ(常数),设D的面积为，则M=μ.o若μ(x,)非常数，仍可用D“分割、求和、近似表示、取极限解决1)分割"No 1,o 2, ., Ao n 用任意曲线网分D为n个小区域相应把薄片也分为小区域HIGH EDUCATION PRESS上页下页返回结束机动目录

有一个平面薄片, 在 xoy 平面上占有区域 D , 度为 计算该薄片的质量 M . 设D 的面积为 , 则 M =   若 非常数 , 仍可用 其面密 解决. 1)“分割” 用任意曲线网分D 为 n 个小区域 , , , ,  1  2   n 相应把薄片也分为小区域 . D 机动 目录 上页 下页 返回 结束 y x “分割、近似表示、求和、取极限

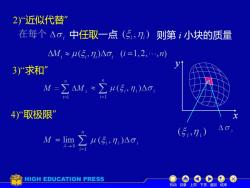
2)近似代替在每个△；中任取一点（i,ni）则第i小块的质量M, ~ μ(5, n)Ao, (i=1,2,,n)3)“求和"M=AM,~Eu(Si,ni)=14)“取极限AO(5,n)nM = limZμ(i,ni)o1-0HIGH EDUCATION PRESS返回结束机动自录上页下页

2)“近似代替” 中任取一点 3)“求和” 4)“取极限” 则第 i 小块的质量 机动 目录 上页 下页 返回 结束 y x

两个问题的共性(1）解决问题的步骤相同“分割、近似代替、求和、取极限(2)所求量的结构式相同曲顶柱体体积nZ=limf(si,n)Ag元→0i=1平面薄片的质量M=limZu(si,ni)Ao1-→01=1HIGH EDUCATION PRESS机动上页下页返回结束自录

两个问题的共性： (1) 解决问题的步骤相同 (2) 所求量的结构式相同 曲顶柱体体积: 平面薄片的质量: 机动 目录 上页 下页 返回 结束 “

二重积分的概念二、:定义：设f(x,J）是定义在有界闭区域 D上的有界函数将区域D任意分成n个小区域△o, (i=1,2,...,n),任取一点（Si,n)E△，作乘积f(i,n)Ao,，并作和Ef(si,n)Ao, 当各小区域最大直径圣元→0时，此和式i=l存在极限，则称极限值为f（x,）在D上的二重积分记作JJ f(x, ydoDHIGHEDUCATION PRESS上页下页返回结束机动自录

二、二重积分的概念 定义: 设 f (x, y) 将区域 D 任意分成 n 个小区域 任取一点 作乘积 ，并作和 在D上的二重积分. 是定义在有界闭区域 D上的有界函数 , 机动 目录 上页 下页 返回 结束 当各小区域最大直径 时，此和式 存在极限，则称极限值为 记作

n f(x,y)do=limf(si,ni)Ao即1→0i=1D其中f(x，)叫做被积函数，f(x，y)dα叫做被积表达式d叫做面积元素，x与叫做积分变量，D叫做积分Zf(i,n)A,叫做积分和区域,i=1HIGH EDUCATION PRESS

即 其中 f (x , y) 叫做被积函数，f (x , y)d 叫做被积表达式 d 叫做面积元素，x 与 y 叫做积分变量，D 叫做积分 区域， 叫做积分和．