《高等数学》课程教学资源（PPT课件）第十章重积分_第四节重积分的应用

第四节重积分的应用曲面的面积质心二三、转动惯量四、引力返回MathGS公式上页下页线与面数学家

第四节 重积分的应用 一、曲面的面积 二、质心 三、转动惯量 四、引力

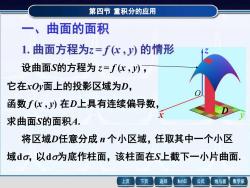
第四节重积分的应用曲面的面积一、1.曲面方程为z=f(x，y）的情形设曲面s的方程为z=f(x，)，它在xOv面上的投影区域为D，函数f(x，J）在D上具有连续偏导数X求曲面S的面积A将区域D任意分成n个小区域，任取其中一个小区域do，以do为底作柱面，该柱面在s上截下一小片曲面上页下页返回MathGS公式数学家线与面

第四节 重积分的应用 x y z O 一、曲面的面积 设曲面S的方程为 z = f (x , y) ， 它在xOy面上的投影区域为D， 函数 f (x , y) 在D上具有连续偏导数， 求曲面S的面积A. D 将区域D任意分成 n 个小区域，任取其中一个小区 域d，以d为底作柱面，该柱面在S上截下一小片曲面. 1. 曲面方程为z = f (x , y) 的情形

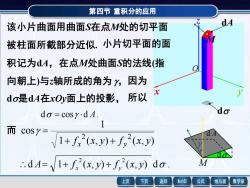
第四节重积分的应用dA该小片曲面用曲面S在点M处的切平面被柱面所截部分近似．小片切平面的面积记为dA，在点M处曲面S的法线（指向朝上)与z轴所成的角为"，因为xdo是dA在xOy面上的投影，所以dado = cosy·d A1而 cos=-1+ fs?(x,y)+ f,?(x,y)doM:.dA=/1+ f'(x,y)+ f'(x,y) do返回MathGS公式线与面数学家上页下页

第四节 重积分的应用 该小片曲面用曲面S在点M处的切平面 被柱面所截部分近似. M dA d 小片切平面的面 积记为dA，在点M处曲面S的法线(指 向朝上)与z轴所成的角为 ，因为 d是dA在xOy面上的投影，  M d A d 所以 d = cos d A. 1 ( , ) ( , ) 1 cos 2 2 f x y f x y + x + y  = d 1 ( , ) ( , ) d . 2 2  A= + f x x y + f y x y  而 x y z O

第四节重积分的应用面积元素dA=/1+f?(x,y)+f?(x,y) do于是曲面S的面积为A= (/1+f(x,y)+f,(x,y) dxdy返回MathGS公式数学家上页下页线与面

第四节 重积分的应用 d 1 ( , ) ( , ) d 2 2 A f x y f x y 面积元素 = + x + y 于是曲面S的面积为 1 ( , ) ( , ) d d . 2 2  = + + D x y A f x y f x y x y

第四节重积分的应用2.曲面方程为x=g，z）的情形若曲面s的方程为x=g(y，z)，它在yOz面上的投影为Dyz，则A= [l /1+g,(y,2)+g.(y,z) dydz返回MathGS公式数学家上页下页线与面

第四节 重积分的应用 2. 曲面方程为x = g (y , z) 的情形 若曲面S的方程为 x = g(y , z)，它在yOz面上的投影 1 ( , ) ( , ) d d . 2 2  = + + Dyz y z A g y z g y z y z 为Dyz，则

第四节重积分的应用3.曲面方程为y=h（x，z）的情形若曲面S的方程为y=h(x，z)，它在xOz面上的投影为Dxz，则A= [ /1+h(x,2)+h?(x,2) dxdzDA返回MathGS公式数学家上页下页线与面

第四节 重积分的应用 3. 曲面方程为y = h (x , z) 的情形 若曲面S的方程为 y = h(x , z)，它在xOz面上的投影 1 ( , ) ( , ) d d . 2 2  = + + Dxz x z A h x z h x z x z 为Dxz，则

第四节重积分的应用4.曲面方程为F(x，y，z)=0的情形若光滑曲面方程为隐式 F(x,y,z2)=0,且 F,≠0,则FFazazX(x, y) e DxyFFaxayZ2AdxdyA=IFDA下页返回MathGS公式数学家上页线与面

第四节 重积分的应用 若光滑曲面方程为隐式 则 x y z y z x x y D F F y z F F x z = −    = −   , , ( , ) d d . | | 2 2 2 x y F F F F A Dxy z x y z  + + = 且 4. 曲面方程为F(x , y , z)=0 的情形

第四节重积分的应用5.曲面方程为参数方程的情形若曲面S的参数方程为x = x(u,v) ,(u,v)e D,y= y(u,v),z = z(u,v) ,其中D是一个平面有界闭区域，又x(u，v)，(u，vz(u，V)在D上具有连续的一阶偏导数，且o(x,y) a(y,z) (z,x)(u,v)a(u,v)a(u,v)返回MathGS公式数学家上页下页线与面

第四节 重积分的应用 5. 曲面方程为参数方程的情形 若曲面S的参数方程为 ( , ) , ( , ) , ( , ) , ( , ) , u v D z z u v y y u v x x u v       = = = 其中D是一个平面有界闭区域，又 x(u , v)， y(u , v) z(u , v) 在D上具有连续的一阶偏导数，且 ( , ) ( , ) , ( , ) ( , ) , ( , ) ( , ) u v z x u v y z u v x y      

第四节重积分的应用不全为零，则曲面S的面积(VEG-F?dudy,A=DE=x+y+zF=x,x,+yuy,+zuz,G=x+y+z返回MathGS公式数学家上页下页线与面

第四节 重积分的应用 不全为零， 则曲面S的面积 . , , d d , 2 2 2 2 2 2 2 v v v u v u v u v u u u D G x y z F x x y y z z E x y z A EG F u v = + + =  +  +  = + + = − 

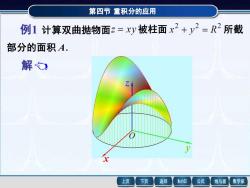
第四节重积分的应用2+2=R2所截例1计算双曲抛物面z=xy被柱面部分的面积A.解白返回MathGS公式上页下页线与面数学家

第四节 重积分的应用 例1 计算双曲抛物面 被柱面 所截 部分的面积 A . 第四节 重积分的应用 解 例1 计算双曲抛物面 z = xy被柱面 2 2 2 x + y = R 所截 曲面在 xOy 面上投影为 : , 2 2 2 D x + y  R 则  = + + D x y A 1 z z dxd y 2 2  = + + D 1 x y dxd y 2 2 r r r R d 1 d 0 2 2π 0  =  + π[(1 ) 1)]. 3 2 2 3 2 = + R − 部分的面积 A . x y z O x y z O