《高等数学》课程教学资源（PPT课件）第十一章 曲线积分与曲面积分_D11_6高斯公式

第十一章第六节高斯公式通量与散度推广公式1公式GaussGreen一、高斯公式通量与散度HIGH EDUCATION PRESS返回结束机动自录上页下页

第六节 Green 公式 Gauss 公式 推广 一、高斯公式 二、通量与散度 机动 目录 上页 下页 返回 结束 高斯公式 通量与散度 第十一章

一、高斯（Gauss）公式定理1设空间闭区域Q由分片光滑的闭曲面Z所围成,, 函数P(x,y,z),Q(x,y,z),R(x,y,z) ，在Q 上有,则有一阶连续偏导数OR2Fdv =Pdydz+Qdzdx+Rdxdy(Gauss 公式)其中是2整个边界曲面的外侧HIGHEDUCATIONPRESS

一、高斯 ( Gauss ) 公式 定理1 设空间闭区域  由分片光滑的 所 ,则有 围成, 函数 (Gauss 公式) 其中 是整个边界曲面的 。 ，在 上有

证明：设Q:z(x,y)≤z(x,y)≤z2(x, y), (x,y)eDxyZ= Zi UZ2 UZ3, Zi : z = zi(x,y), Z2 : z = z2(x,y)T22(x,y)oRaR一Z245则dxdydzdyazzi(x,y)2DOxWW)?[(R(x, y, 22(x, y))- R(x, y, zi(x, y)) )d xd yD2Dxyf Rdxrdy =RdxdyRdxdy+Rdxdy+xZ3Z=-R(x, y, zi(x, y)d xdy +R(x, y,z2(x, y))dxdyDDXORJdv=§Rdxdy所以07HIGH EDUCATION PRESS

2 3 1  z y x Dxy R(x, y, )− R(x, y, ) d xd y : ( , ), 1 1  z = z x y 证明: 设 ,  = 12 3 z z z x y R z x y d ( , ) ( , ) 2 1    ( , ) 2 z x y ( , ) 1 z x y : ( , ), 2 2  z = z x y 则 R(x, y, z 1 (x, y))d xdy R(x, y, z2 (x, y ))dxdy 所以

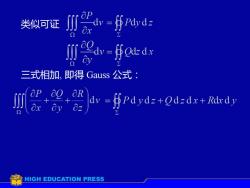
ap-dv =f Pdydz川类似可证oxdv= fQd dxO即得 Gauss 公式：三式相加，apaRaodv =Pdydz+Qdzdx+ RdxdyoxQHIGH EDUCATION PRESS

类似可证 三式相加, 即得 Gauss 公式：

F(x-y)dxdy+(y-2)xdydz例1 用Gauss公式计算其中为柱面=1及平面z = 0,z=3所围空间Ix+v:闭域Q的整个边界曲面的外侧令P=(y-z)x, Q=0, R=x-y解：apaRa则=0由Gauss公式oxozJJ (y-2)dv原式=29元" do[pd p(psin0-2) dz =思考：若Z改为内侧，结果有何变化？若乙为圆柱侧面(取外侧），如何计算HIGH EDUCATION PRESS

例1 用Gauss 公式计算 其中 为柱面 闭域  的整个边界曲面的外侧. 解: 令 由Gauss 公式 原式 = x 3 o z 1 y P = (y − z)x, Q = 0, R = x − y 及平面 z = 0 , z = 3 所围空间 思考: 若  改为内侧, 结果有何变化? 若  为圆柱侧面(取外侧) , 如何计算? 则

例2计算(2x+z)dydz+zdxdy,其中z为曲面z=x2+2(0≤z≤1)的上侧。添加辅助面Z：z=1（x2+2≤1）上侧解：令P=2x+z,Q=0,R=zyapaRao则公式由Gauss.0axaz3dv=[[(2x+z)dydz+zdxdy =2doodp3元22+Z123元3元元ldxdy-l/(2x+z)dydz+zdxdy原式1222D7XHIGH EDUCATION PRESS

例2 解: 添加辅助面 令 则 由Gauss 公式 原式=

(xcosα+ycosβ+zcosy)ds例3公式计算积分利用Gauss其中为锥面x2+2=2介于z=0及Zhh之间部分的下侧Z=Z解：作辅助面Zi:z=h,（x2+y2≤h）取上侧y由Gauss 公式令P=x2, Q=y2, R=z?(x cosα+y° cosβ+2 cosy)dS =2f(zdy(x+y+z)dv=222+h4"del"pdp]zdz[(x cosa+y' cosβ+z.cosy)dS =[2 dS=[[H dxdy= h而DAZ元h4元h4=-元h原式=HIGHEDUZATION PRESS

例3 利用Gauss 公式计算积分 其中  为锥面 2 2 2 x + y = z  h o z y x 解: 作辅助面 : , 1 z = h 取上侧 介于 z = 0 及 z = h 之间部分的下侧. 1 h 令 由Gauss 公式 而 原式=

使用Gauss公式应注意的条件aRD连续az2.Z为闭曲面3.Z为闭曲面的外侧HIGH EDUCATION PRESS

使用Gauss公式应注意的条件

二、通量与散度Gauss公式的物理意义aRapdodv=Pdydz+Qdzdx+Rdxdy(1dx2O设稳定流动的不可压缩流体的密度为1，速度场为=Pi+Qj+Rkn=cosαi+cosβj+cos yk式右端表示单位时间内流体经过乙流向指定侧的流量，1即单位时间内离开闭区域Q的流体总质量：式左端表示分布在Q内的源头在单位时间内所产生的流体总质量HIGH EDUCATION PRESS

二、通量与散度 Gauss公式的物理意义 设稳定流动的不可压缩流体的密度为1, 速度场为 ① ① 式右端表示单位时间内流体经过流向指定侧的流量， 即单位时间内离开闭区域的流体总质量； ① 式左端表示分布在内的源头在单位时间内所产生的 流体总质量

定义：设有向量场A(x, y,z) = P(x,y,z)i+Q(x, y,z) j+ R(x, y,z)k其中P,Q,R具有连续一阶偏导数,Z 是场内的一片有向I曲面,其单位法向量n，则称A.nds为向量场A通过Z有向曲面的通量（流量）在场中点 M(x,y,2)处aP.oQaR记作divAaxaya2称为向量场A在点M的散度（divergence)HIGH EDUCATION PRESS

定义: 设有向量场 A(x, y,z) = P(x, y,z)i + Q(x, y,z) j + R(x, y,z) k 其中P, Q, R 具有连续一阶偏导数, 是场内的一片有向 曲面, 其单位法向量 n, 则称 为向量场 A 通过 有向曲面  的通量(流量) . 在场中点 M(x, y, z) 处 称为向量场 A 在点 M 的散度（divergence) 记作 div A z R y Q x P   +   +  