《高等数学》课程教学资源（习题课）D9习题课

第八章习题课元函数微分法n基本概念二、多元函数微分法三、多元函数微分法的应用四、练习题HIGH EDUCATION PRESS返回结束机动自录上页下页

习题课 第八章 机动 目录 上页 下页 返回 结束 一、 基本概念 二、多元函数微分法 三、多元函数微分法的应用 多元函数微分法 四、练习题

基本概念及问题一、极限、连续1.二元函数的定义、·求定义域·判断极限不存在及求极限的方法·函数的连续性及其性质2.偏导数与全微分·计算偏导数与全微分3.方向导数与梯度·计算方向导数与梯度4.二元函数的驻点与极值点极值的计算HIGH EDUCATION PRESS返回结束机动目录上页下页

一、基本概念及问题 1. 二元函数的定义、极限 、连续 • 求定义域 • 判断极限不存在及求极限的方法 • 函数的连续性及其性质 2. 偏导数与全微分 机动 目录 上页 下页 返回 结束 • 计算偏导数与全微分 3. 方向导数与梯度 • 计算方向导数与梯度 4. 二元函数的驻点与极值点 • 极值的计算

5.几个基本概念的关系连续性偏导数存在方向导数存在可微性HIGH EDUCATION PRESS

连续性 偏导数存在 方向导数存在 可微性 5. 几个基本概念的关系

多元函数微分法二、显示结构1.分析复合结构画变量关系图隐式结构自变量与因变量由所求对象判定2.正确使用求导法则分段用乘,分叉用加,单路全导叉路偏导注意正确使用求导符号3.利用一阶微分形式不变性HIGH EDUCATION PRESS返回结束机动目录上页下页

二、多元函数微分法 显示结构 隐式结构 1. 分析复合结构 (画变量关系图) 自变量与因变量由所求对象判定 2. 正确使用求导法则 “分段用乘,分叉用加,单路全导,叉路偏导” 注意正确使用求导符号 3. 利用一阶微分形式不变性 机动 目录 上页 下页 返回 结束

三、多元函数微分法的应用1.在几何中的应用求曲线在切线及法平面(关键:抓住切向量）(关键抓住法向量）求曲面的切平面及法线2.极值与最值问题，极值存在的必要条件与充分条件（代入法，拉格朗日乘数法）求条件极值的方法·求解最值问题HIGHEDUCATION PRESS返回结束机动目录上页下页

三、多元函数微分法的应用 1.在几何中的应用 求曲线在切线及法平面 (关键: 抓住切向量) 求曲面的切平面及法线 (关键: 抓住法向量) 2. 极值与最值问题 • 极值存在的必要条件与充分条件 • 求条件极值的方法 (代入法, 拉格朗日乘数法) • 求解最值问题 机动 目录 上页 下页 返回 结束

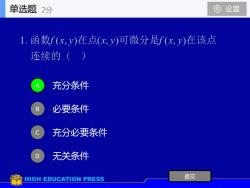
单选题0设置.2分1.函数f(x,y)在点(x,y)可微分是f(x,y)在该点连续的（充分条件必要条件充分必要条件无关条件提交HIGHEDUCATION PRESS

充分条件 必要条件 充分必要条件 无关条件 A B C D 提交 单选题 2分

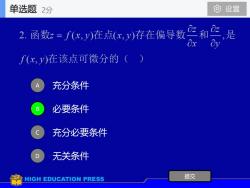
单选题0设置2分2和是2. 函数z=f(x,y)在点(x,J)存在偏导数OxOyf(x,y)在该点可微分的（充分条件必要条件充分必要条件无关条件提交HIGHEDUCATION PRESS

充分条件 必要条件 充分必要条件 无关条件 A B C D 提交 单选题 2分

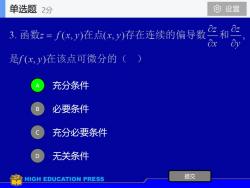
单选题0设置2分一zOz和3. 函数z=f(x,y)在点(x,y)存在连续的偏导数OyOx是f(xy)在该点可微分的（充分条件必要条件充分必要条件无关条件提交HIGHEDUCATION PRESS

充分条件 必要条件 充分必要条件 无关条件 A B C D 提交 单选题 2分

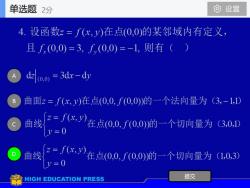
单选题设置2分4.设函数z=f(x,y)在点(0,0)的某邻域内有定义，且J(0,0)=3,f,(0,0)=-1, 则有（dz[(o,0) = 3dx- dy曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为(3,-1,1)z= f(x,y)曲线在点(0,0,f(0,0))的一个切向量为可(3,0,1)y=0z=f(x,y)曲线在点(0,0,f(0,0))的一个切向量为（1,0,3）=0提交HIGH EDUCATION PRESS

A B C D 提交 单选题 2分

例1设函数f存在二阶连续（偏）导数，计算OxOyz= f(x+2z= f(xHIGHEDUCATION PRESS机动目录上页下页返回结束

例1 设函数 f 存在二阶连续（偏）导数，计算 (3) ( , ) (2) ( ) (1) ( ) 2 2 2 x y z f x x y z f x x y z x f = = + = 机动 目录 上页 下页 返回 结束