《高等数学》课程教学资源（PPT课件）第十一章 曲线积分与曲面积分_D11-5对坐标的曲面积分

第十一章第五节对坐标的曲面积分有向曲面一、二、对坐标的曲面积分的概念与性质三、对坐标的曲面积分的计算法四、两类曲面积分的联系HIGH EDUCATION PRESS返回结束机动目录上页下页

第五节 一、有向曲面 二、 对坐标的曲面积分的概念与性质 三、对坐标的曲面积分的计算法 四、两类曲面积分的联系 机动 目录 上页 下页 返回 结束 对坐标的曲面积分 第十一章

一、有向曲面双侧曲面·曲面分类曲面分内侧和单侧曲面外侧曲面分左侧和曲面分上侧和莫比乌斯带右侧下侧（单侧曲面的典型HIGH EDUCATION PRESS

一、有向曲面 • 曲面分类 双侧曲面 单侧曲面 莫比乌斯带 曲面分上侧和 下侧 曲面分内侧和 外侧 曲面分左侧和 (单侧曲面的典型) 右侧

其方向用法向量指向·指定了侧的曲面叫有向曲面表示：COSYcosβcosα方向余弦封闭曲面外侧>0 为前侧>0 为右侧>0为上侧侧的规定内侧<0 为后侧<0 为左侧<0为下侧HIGH EDUCATION PRESS

其方向用法向量指向 方向余弦 > 0 为前侧 0 为右侧 0 为上侧 < 0 为下侧 外侧 内侧 侧的规定 • 指定了侧的曲面叫有向曲面, 表示 :

·设Z为有向曲面.面积元素^S在xoy面上的投影为的面积为(△）x≥0,规定(△S)xy, (△S)x(△o )xy,当cos>O时(△S)xy =^-(△α )xy,当cos<O时当cos=O时?(△S) yz, (△S),类似可规定171HIGH EDUCATION PRESS

• 设  为有向曲面,面积元素 ( ) , S xy S (S) xy = 在 xoy 面上的投影为 的面积为 规定 ( ) ,  xy ( ) , −  xy 0 , 当cos  0时 当cos  0时 当cos  0时 类似可规定 S yz S zx ( ) , ( )

对坐标的曲面积分的概念与性质二、引例设稳定流动的不可压缩流体的速度场为=(P(x,y,z), Q(x,y,z), R(x,y,z))求单位时间流过有向曲面乙的流量Φn分析：若Z是面积为S的平面法向量：n=(cosα,cosβ,cosy）O流速为常向量：√S则流量Φ=S.vcose =Sv. nHIGH EDUCATION PRESS

二、 对坐标的曲面积分的概念与性质 引例 设稳定流动的不可压缩流体的速度场为 求单位时间流过有向曲面  的流量 . S  分析: 若  是面积为S 的平面, 则流量 法向量: 流速为常向量: n v

对一般的有向曲面之，对稳定流动的不可压缩宿流体的速度场v=(P(x,y,z), Q(x,y,z), R(x,y,z))方法：“分割，近似表示，求和,取极限"N设 n; = (cosαi, cos βi, cos Yi), =(P(5,n,5), Q(S,n,5), R(,ni,5))ZnE[ P(Ei, ni,Si)cosα; +Q(Ei, ni,Si)cos βilimΦ= 1-0i=1+ R(Ei, ni,S,)cos Yi JASnlim二Z[ P(5i, ni,Si)(ASi) yz +Q(5i, ni,Si)(AS,)zx10i=1+R(5i,ni,S)(AS)xy ]cosy,AS, ~(AS,)x其中HIGHEDUCATION PRESS

 对一般的有向曲面 , 方法：“分割，近似表示，求和, 取极限” 0 lim → =   = n i 1  P i i  i i ( , , )cos R i i i i + ( , , )cos 0 lim → =   = n i 1 Q i i  i i + ( , , )cos Si 对稳定流动的不可压缩流体的 速度场 ni i v (cos , cos , cos ) ni i i i 设 =     其中

设Z为光滑的有向曲面,R(x,y,)在Z上有界，定义任意分割Z为n小块，△S，记△S）为△S在xoy面上的投影，任意取点（,nS）E△S,，当→0时，极限nlimR(5i,ni,S,)(△S,)x, 存在2元-0i=-1则称此极限为函数R(x,y,z)在有向曲面Z上对坐标x,y曲面积分，或第二类曲面积分。R(x, y,z)dxdy记作[[(x, y, z)dzdx/P(x, y,z)dydz,类似可定义AHIGHEDUCATIONPRESS

设  为光滑的有向曲面, 在  上有界， 记作 曲面积分，或第二类曲面积分。 则称此极限为函数 在有向曲面  上对坐标 x,y 定义 任意分割  为 n小块， 任意取点 ，当 时，极限 存在 类似可定义

注：1.被积函数在积分曲面Z上连续时一定可积；I Pdydz + Qdzdx + Rdxdy2.组合曲面积分：3.应用（求流量）：Φ=「[Pdydz+Qdzdx+Rdxdy4.积分关于积分曲面的可加性；5.用>表示>的反向曲面，则R(x, y,z)dxdy=-1R(x, y,z)dxdyHIGH EDUCATION PRESS

注： 1. 被积函数在积分曲面 上连续时一定可积； 2. 组合曲面积分： 3. 应用（求流量）： 4. 积分关于积分曲面的可加性； 5. 用 ˉ 表示  的反向曲面, 则

三、对坐标的曲面积分的计算法------化为二重积分Z:z= z(x,y), (x,y)eDxy取上侧1．设积分曲面R(x,y,z)是Z上的连续函数,则R(x, y,z)dxdy =R[x,y,z(x,y)]dxdyy匕为下侧时R(x, y,z)dxdy = -// R(x, y, z(x, y)dxdyD（上正下负）HIGH EDUCATION PRESS

三、对坐标的曲面积分的计算法- 1. 设积分曲面 取上侧, 是  上的连续函数, 则 为下侧时 （上正下负）

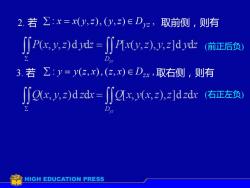
2. 若 Z:x=x(y,z),(y,2)eDyz，取前侧，则有[P(x, y,z)d ydz = //P[x(y,z),y,z]d ydz(前正后负)DyZ:y=y(z,x),(z,x)E Dzx,取右侧，则有3.若[[O(x, y,z)d zdx=J[g[x, y(x,z),z]d zdx(右正左负)DVZHIGH EDUCATION PRESS

2. 若 取前侧，则有 3. 若 取右侧，则有 (前正后负) (右正左负)