《高等数学》课程教学资源（PPT课件）第十章 重积分_10_4重积分的应用

第十章第四节重积分的应用一、立体体积曲面的面积三、物体的质心四、物体的转动惯量五、物体的引力HIGH EDUCATION PRESS返回结束机动自录上页下页

第四节 一、立体体积 二、曲面的面积 三、物体的质心 四、物体的转动惯量 五、物体的引力 机动 目录 上页 下页 返回 结束 重积分的应用 第十章

一、立体体积·曲顶柱体的顶为连续曲面 z=f(x,y),(x,y)ED则其体积为V = JJ f(x, y)doD·占有空间有界域Q的立体的体积为dxdydz一HIGH EDUCATION PRESS机动上页下页返回结束自录

一、立体体积 • 曲顶柱体的顶为连续曲面 则其体积为 • 占有空间有界域  的立体的体积为 机动 目录 上页 下页 返回 结束

二、曲面的面积设光滑曲面S:z= f(x,y),(x,y)eDSMS则面积A可看成曲面上各点 M(x,y,z)处小切平面的面积dA无限积累而成设它在D 上的投影为 do，则dado =cosy.d AnCOSY=1+ fx(x,y)+ f,(x,y)C/1+ fx(x,y)+f,'(x,y) dodA=1Mdo（称为面积元素）HIGH EDUCATION PRESS上页下页返回结束机动目录

 M d A z d n 二、曲面的面积 x y z S o 设光滑曲面 则面积 A 可看成曲面上各点 M (x, y,z) 处小切平面的面积 d A 无限积累而成. 设它在 D 上的投影为 d , d = cos d A 1 ( , ) ( , ) 1 cos 2 2 f x y f x y + x + y  = d 1 ( , ) ( , ) d 2 2 A f x y f x y = + x + y (称为面积元素) 则   M n  d 机动 目录 上页 下页 返回 结束

故有曲面面积公式A= f /1+f(x,y)+ f,'(x,y) do即dxdyHIGH EDUCATION PRESS机动目录上页返回结束下页

故有曲面面积公式 即 机动 目录 上页 下页 返回 结束

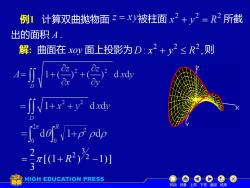
例1计算双曲抛物面z=xy被柱面2+2=R2所截出的面积 A解：曲面在 xoy面上投影为D:x2+2≤R2,则dxdy福1+x? +y?dxdyRde1+ppdp元[(1+ R2) -1)]HIGH EDUCATION PRESS上页下页返回结束机动自录

例1 计算双曲抛物面 被柱面 所截 解: 曲面在 xoy 面上投影为 : , 2 2 2 D x + y  R 则 [(1 ) 1)] 3 2 2 3 2 =  + R − 出的面积 A . 机动 目录 上页 下页 返回 结束

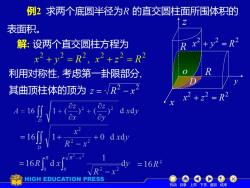
例2求两个底圆半径为R的直交圆柱面所围体积的表面积。R x+y?=R解：设两个直交圆柱方程为x? +y2 =R?, x?+2? = RR利用对称性，考虑第一卦限部分其曲顶柱体的顶为z=/R2-x2x2 + z? = R2A=16dxdy=16+0dxdyDR=16R=16R2ddyXLrHIGHEDUCATIONPRESS上页下页返回结束机动自录

机动 目录 上页 下页 返回 结束 例2 求两个底圆半径为R 的直交圆柱面所围体积的 表面积。 解: 设两个直交圆柱方程为 利用对称性, 考虑第一卦限部分, 其曲顶柱体的顶为

例3.设有一颗地球同步轨道通信卫星距离地面高度为h=36000km.运行的角速度与地球自转的角速度相同，试计算该卫星的覆盖面积与地球表面积的比值（地球半径R=6400km）解: Z: z=/ R?-x2-y2Dry:x?+y?≤Rsinαdxdy一+Rd.xdyR?-x?-yHIGHEDUCATIONPRESS上页下页返回结束机动自录

例3. 设有一颗地球同步轨道通信卫星距离地面高度 为 h = 36000 km, 运行的角速度与地球自转的角速度相 同，试计算该卫星的覆盖面积与地球表面积的比值。 （地球半径R = 6400 km) 机动 目录 上页 下页 返回 结束 解:

RRsina2元depdpJoR-p?Rsino=2元R(-/R-p)=2元R(1-cosα)RR2元R2hA=2元R.COSα=R+hR+hR+h所求比值为36×106hA42.5%2(36 + 6.4)×1064元R2(R +h)HIGH EDUCATION PRESS

所求比值为

三、物体的质心1.平面薄片的质心(x,y),i=1,2,,n，质量分别为设平面上的质点系m.,i=1,2,,n，由力学可知该质点系的质心坐标为证nZZm,ximyiMMi1-1x=7nnMMVZm;miili=l其中M为质点系的总质量，M,M分别为质点系对v轴和x轴的静矩HIGH EDUCATION PRESS

三、物体的质心 设平面上的质点系 ，质量分别为 ，由力学可知, 该质点系的质心坐标为 其中M 为质点系的总质量， 分别为质点系对 1. 平面薄片的质心

设平面薄片D的面密度函数为μ(x,，（在D上连续福dM, = xμ(x,y)do, dMx = yμ(x,y)do静矩元素则xu(x,y)do, M, =l yu(x,y)doM=DDM = ( μ(x, y)do质心坐标为xu(x,y)doyu(x,y)doMMx =V=MMμu(x, y)dou(x,y)doDDHIGH EDUCATION PRESS上页下页返回结束机动自录

机动 目录 上页 下页 返回 结束 设平面薄片D的面密度函数为 ,（在D上连续） 静矩元素 则 质心坐标为