《高等数学》课程教学资源（PPT课件）第十一章曲线积分与曲面积分_第七节斯托克斯公式、环流量与旋度

第七节斯托克斯公式环流量与旋度一、斯托克斯公式*二、空间曲线积分与路径无关的条件三、环流量与旋度返回MathGS公式上页下页线与面数学家

第七节 斯托克斯公式 环流量与旋度 一、斯托克斯公式 *二、空间曲线积分与路径无 关的条件 *三、环流量与旋度

第七节斯托克斯公式环流量与旋度一、斯托克斯公式(Stokes）斯托克斯(Stokes)公式是格林公式的推广．格林公式表达了平面闭区域上的二重积分与其边界曲线上的曲线积分间的关系，而斯托克斯公式则把曲面上的曲面积分与沿着乙的边界曲线的曲线积分联系起来下页返回MathGS公式数学家上页线与面

第七节 斯托克斯公式 环流量与旋度 一、斯托克斯公式(Stokes) 斯托克斯 (Stokes)公式是格林公式的推广. 格林公 式表达了平面闭区域上的二重积分与其边界曲线上的 曲线积分间的关系， 而斯托克斯公式则把曲面上的 曲面积分与沿着 的边界曲线的曲线积分联系起来

第七节斯托克斯公式环流量与旋度定理1设是分段光滑的空间有向闭曲线，Z是以厂为边界的分片光滑的有向曲面，厂的正向与的侧符合右手规则,函数 P(x,,z)、Q(x,,z)、R(x,,z)在曲面（连同边界厂）上具有一阶连续偏导数，则有ORapORaQapaQdxdydydz+dzdx+ayazOzOxaxOyPdx+Qdy+Rdz证明包板书包斯托克斯公式返回MathGS公式上页下页线与面数学家

第七节 斯托克斯公式 环流量与旋度 定理1 设 是分段光滑的空间有向闭曲线，  是以  为边界的分片光滑的有向曲面， 函数 P(x , y , z)、Q(x , y , z)、R(x , y , z) 在 曲面 (连同边界 )上具有一阶连续偏导数，则有 d d d . d d d d d d   = + +           −    +        −   +           −   Γ Σ P x Q y R z x y y P x Q z x x R z P y z z Q y R 第七节 斯托克斯公式 环流量与旋度 证明 情形1 设 与平行 z 轴的直线相交不多于一点, 设其方程为 : ( , ), ( , ) , Dx y Σ z = f x y x y  取上侧 (如图).  的正向边界曲线 在 xOy 面上的投 影为平面有向曲线C. 下面利用两类曲面积之间的联系 以及格林公式，证明   n Dxy C x z O 第七节 斯托克斯公式 环流量与旋度 板书证明 定理1 设 是分段光滑的空间有向闭曲线，  是以  为边界的分片光滑的有向曲面， 函数 P(x , y , z)、Q(x , y , z)、R(x , y , z) 在 曲面 (连同边界 )上具有一阶连续偏导数，则有  的正向与 的侧符 合右手规则，   n Dxy C x z O  的正向与的侧符 合右手规则， 斯托克斯公式

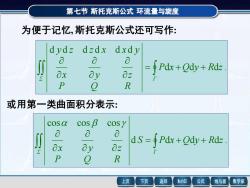
第七节斯托克斯公式环流量与旋度为便于记忆，斯托克斯公式还可写作：dydz dzdx dxdyaaaPdx +Qdy+ RdzaxOzoyZPQR或用第一类曲面积分表示：cOsBCOSYCOSαaaad S = $ Pdx + Qdy+ Rdz .oxOzoyZP0R下页返回MathGS公式数学家上页线与面

第七节 斯托克斯公式 环流量与旋度 为便于记忆, 斯托克斯公式还可写作:   = + +       Σ Γ P x Q y R z P Q R x y z y z z x x y d d d . d d d d d d 或用第一类曲面积分表示: d d d d . cos cos cos   = + +       Σ Γ S P x Q y R z P Q R x y z   

第七节斯托克斯公式环流量与旋度ORapORapQ00dxdydzdx+dydz+axoyOzzOxoyZ$Pdx+Qdy+Rdz在斯托克斯公式中，如果z=常数，即是平行于xOy面的平面，则斯托克斯公式就变成apa0Jdxdy = $Pdx +QdyaxayD这就是格林公式，所以，格林公式是斯托克斯公式的特殊情形，上页下页返回MathGS公式数学家线与面

第七节 斯托克斯公式 环流量与旋度 d d d . d d d d d d   = + +           −    +        −   +           −   Γ Σ P x Q y R z x y y P x Q z x x R z P y z z Q y R 在斯托克斯公式中，如果 z = 常数，即 是平行于 xOy 面的平面，则斯托克斯公式就变成 d d d d ,   = +           −   D L x y P x Q y y P x Q 这就是格林公式．所以，格林公式是斯托克斯公式的 特殊情形．

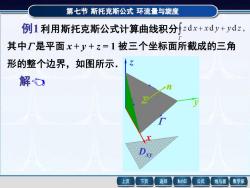
第七节斯托克斯公式环流量与旋度例1利用斯托克斯公式计算曲线积分zdx+xdy+ydz,其中厂是平面x+V+z=1被三个坐标面所截成的三角形的整个边界，如图所示.解mST十返回MathGS公式上页下页线与面数学家

第七节 斯托克斯公式 环流量与旋度 例1 利用斯托克斯公式计算曲线积分 其中 是平面 x + y + z = 1 被三个坐标面所截成的三角 形的整个边界，如图所示． 第七节 斯托克斯公式 环流量与旋度 解 其中 是平面 x + y + z = 1 被三个坐标面所截成的三角 形的整个边界，如图所示． 由斯托克斯公式，得  + + Γ z d x x d y y d z        = Σ z x y x y z d y d z d z d x d x d y  = + + Σ d y d z d z d x d x d y  = Σ 3 d x d y  = Dxy 3 d x d y . 2 3 = 由对称性 例1 利用斯托克斯公式计算曲线积分  + + Γ z d x x d y y d z ,   n Dxy x y z   n Dxy x y z

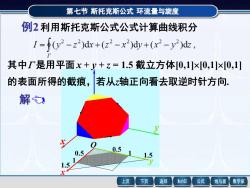
第七节斯托克斯公式环流量与旋度例2利用斯托克斯公式公式计算曲线积分[= $(y2 -z°)dx+(z? -x)dy+(x? - y)dz ,其中┌是用平面x + y+z =1.5 截立方体[0,1]×[0,1]×[0,1]的表面所得的截痕，若从轴正向看去取逆时针方向解台00.50.51.51.5返回MathGS公式上页下页线与面数学家

第七节 斯托克斯公式 环流量与旋度 O x y 1.5 1.5 1 0.5 1 0.5 x y 例2 利用斯托克斯公式公式计算曲线积分 其中 是用平面 x + y + z = 1.5 截立方体[0,1][0,1][0,1] 的表面所得的截痕，若从z轴正向看去取逆时针方向. 第七节 斯托克斯公式 环流量与旋度 O x y 1.5 1.5 1 0.5 1 0.5 x y 解 例2 利用斯托克斯公式公式计算曲线积分 ( )d ( )d ( )d , 2 2 2 2 2 2  = − + − + − Γ I y z x z x y x y z 其中 是用平面 x + y + z = 1.5 截立方体[0,1][0,1][0,1] 的表面所得的截痕，若从z轴正向看去取逆时针方向. 取 为平面x + y + z = 1.5 的上侧被 所围成的部分，则  的单位法向量为 . 3 1 , 3 1 , 3 1      

第七节斯托克斯公式环流量与旋度二、空间曲线积分与路径无关的条件定理2设空间区域G是一维单连通域，函数P(x,y,z)Q(x,y,z),R(x,y,z)在G内具有一阶连续偏导数，则空间曲线积分Pdx+Qdy+Rdz在G内与路径无关的充分必要条件是在G内恒有apapaRaRraoaxOzOZoyOyOx证明返回MathGS公式下页线与面数学家上页

第七节 斯托克斯公式 环流量与旋度 *二、空间曲线积分与路径无关的条件 定理2 设空间区域G是一维单连通域，函数P(x, y, z) Q(x, y, z), R(x, y, z)在G内具有一阶连续偏导数，则空间 曲线积分  + + Γ Pdx Qdy Rdz 在G内与路径无关的充分必要 条件是在G内恒有 , , . z P x R y R z Q x Q y P   =     =     =   第七节 斯托克斯公式 环流量与旋度 证明 充分性 若在G内恒有 , , , z P x R y R z Q x Q y P   =     =     =   则由斯托克斯公式，有  + + Γ Pdx Qdy Rdz            −    +        −   +           −   = Σ x y y P x Q z x x R z P y z x Q y R d d d d d d = 0

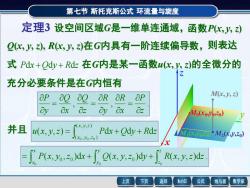
第七节斯托克斯公式环流量与旋度定理3设空间区域G是一维单连通域，函数P(x,y，z)Q(xy,z)R(x,y,z)在G内具有一阶连续偏导数，则表达式Pdx+Ody+Rdz在G内是某一函数u(x,y,z）的全微分的7充分必要条件是在G内恒有M(x,y,z)apapaRaRdO0OOZOZoxMo(xoyo,zo)中(x.y,=)并且Pdx+Qdy+Rdzu(x,y,z)=M(xyeM(xy,zo)J(xoyo,-o）XP(x, yo,zo)dx + Q(x, y,zo)dy+ R(x, y,z)dzMathGS公式上页下页返回线与面数学家

第七节 斯托克斯公式 环流量与旋度 定理3 设空间区域G是一维单连通域，函数P(x, y, z) Q(x, y, z), R(x, y, z)在G内具有一阶连续偏导数，则表达 式 Pdx +Qdy + Rdz 在G内是某一函数u(x, y, z)的全微分的 充分必要条件是在G内恒有 , , . z P x R y R z Q x Q y P   =     =     =   并且  = + + ( , , ) ( , , ) 0 0 0 ( , , ) d d d x y z x y z u x y z P x Q y R z ( , , )d ( , , )d ( , , )d . 0 0 0  0 0  0  = + + z z y y x x P x y z x Q x y z y R x y z z M(x, y, z) M0 (x0 ,y0 ,z0 ) M1 (x,y0 ,z0 ) M2 (x,y,z0 ) x y z

第七节斯托克斯公式环流量与旋度*三、环流量与旋度斯托克斯公式aRapaRapQaQdxdy=$Pdx +Ody+Rdzdzdx+dydz+Ozzaxaxayoy设曲面的法向量为n = (cos α, cos β, cos )曲线厂的单位切向量为 t = (cos a, cos μ, cosv)则斯托克斯公式可写为apOR0gapgORJ,[Ccos JdscosBcosaα+aoz0xax701f,(Pcos a+Qcos μ+ Rcosv)ds.下页返回MathGS公式数学家上页线与面

第七节 斯托克斯公式 环流量与旋度 *三、 环流量与旋度 斯托克斯公式 设曲面  的法向量为 曲线  的单位切向量为 则斯托克斯公式可写为 ( cos cos cos )d .  = + + Γ P  Q  R  s n = (cos, cos , cos ) , τ = (cos, cos, cos ). d d d d d d d d d .   = + +           −    +        −   +           −   Σ Γ x y P x Q y R z y P x Q z x x R z P y z z Q y R